本试卷分第I卷(选择题)和第II卷(非选择题)两部分。第I卷1至2页。第II卷3至8页。
共150分。考试时间120分钟。
第I卷(选择题共60分)
注意事项:
l.答第I卷前,考生务必将自己的姓名、准考证号、考试科目、试卷类型(A或B)用铅笔涂
写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦
干净后。再选涂其它答案,不能答在试题卷上。
3.考试结束,监考人将本试卷和答题卡一并收回。
参考公式: 正棱台、圆台的侧面积公式
三角函数的积化和差公式
sinαcosβ=[sin(α+β)+sin(α-β)]/2 cosαsinβ=[sin(α+β)-sin(α-β)]/2
cosαcosβ=[cos(α+β)+cos(α-β)]/2 sinαsinβ=-[cos(α+β)-cos(α-β)]/2
正棱台、圆台的侧面积公式:
S台侧=(c'+c)L/2 其中c'和c表示圆台的上下底面的周长,L表示斜高或母线长。
台体的体积公式: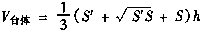 其中s,s'分别表示上下底面积,h表示高。
一. 选择题:本大题共14小题;第(1)―(1O)题每小题4分,第(11)―(14)题每小题5分,共60分
在每小题给出的四个选顶中,只有一顶是符合题目要求的。 其中s,s'分别表示上下底面积,h表示高。
一. 选择题:本大题共14小题;第(1)―(1O)题每小题4分,第(11)―(14)题每小题5分,共60分
在每小题给出的四个选顶中,只有一顶是符合题目要求的。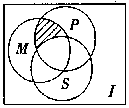 (1)如图,I是全集,M、P、S是I的3个子集,则阴影部分所表示的集合是
(A)(M∩P〕∩S (B)(M∩P)∪S
(C〕(M∩P)∩
(1)如图,I是全集,M、P、S是I的3个子集,则阴影部分所表示的集合是
(A)(M∩P〕∩S (B)(M∩P)∪S
(C〕(M∩P)∩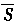 (D〕(M∩P)∪ (D〕(M∩P)∪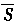 (2)已知映射f:A→B,其中,集合A={-3,-2,-1,1,2,3,4},集合B中的元素都是A中
元素在映射f下的象,且对任意的a∈A,在B中和它对应的元素是|a|,则集合B中元素
的个数是
(A)4 (B)5 (C)6 (D)7
(3)若函数y=f(x)的反函数是y=g(x),f(a)=b,ab≠0,则g(b)等于
(A)a (B)a-1 (C)b (D)b-1
(4)函数f(x)=Msin(ωx+ρ)(ω>0)在区间[a,b]上是增函数,且f(a)=-M,f(b)=M,
则函数g(x)=Mcos(ωx+ρ)在[a,b]上
(A)是增函数 (B)是减函数
(C)可以取得最大值M (D)可以取得最小值-M
(5)若f(x)sinx 是周期为∏的奇函数,则f(x)可以是
(A)sinx (B)cosx (C)sin2x (D)cos2x
(6)曲线x2+y2+2
(2)已知映射f:A→B,其中,集合A={-3,-2,-1,1,2,3,4},集合B中的元素都是A中
元素在映射f下的象,且对任意的a∈A,在B中和它对应的元素是|a|,则集合B中元素
的个数是
(A)4 (B)5 (C)6 (D)7
(3)若函数y=f(x)的反函数是y=g(x),f(a)=b,ab≠0,则g(b)等于
(A)a (B)a-1 (C)b (D)b-1
(4)函数f(x)=Msin(ωx+ρ)(ω>0)在区间[a,b]上是增函数,且f(a)=-M,f(b)=M,
则函数g(x)=Mcos(ωx+ρ)在[a,b]上
(A)是增函数 (B)是减函数
(C)可以取得最大值M (D)可以取得最小值-M
(5)若f(x)sinx 是周期为∏的奇函数,则f(x)可以是
(A)sinx (B)cosx (C)sin2x (D)cos2x
(6)曲线x2+y2+2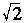 x-2 x-2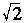 y=0关于
(A)直线x=轴对称 (B)直线y=-x轴对称
(C)点(-2, y=0关于
(A)直线x=轴对称 (B)直线y=-x轴对称
(C)点(-2,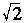 )中心对称 (D)点(- )中心对称 (D)点(-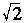 ,0)中心对称
(7)若干毫升水倒人底面半径为2cm的圆柱形器皿中,量得水面的高为6cm,若将这些水倒
人轴截面是正三角形的倒圆锥形器皿中,则水面的高度是
(A)6 ,0)中心对称
(7)若干毫升水倒人底面半径为2cm的圆柱形器皿中,量得水面的高为6cm,若将这些水倒
人轴截面是正三角形的倒圆锥形器皿中,则水面的高度是
(A)6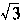 cm (B)6cm (C)2 cm (B)6cm (C)2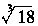 cm (D)3 cm (D)3 cm
(8)若(2x+ cm
(8)若(2x+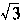 )3=a0+a1x+a2x2+a3x3,则(a0+a2)2-(a1+a3)2的值为
(A)-1 (B)l (C) 0 (D) 2
(9)直线 )3=a0+a1x+a2x2+a3x3,则(a0+a2)2-(a1+a3)2的值为
(A)-1 (B)l (C) 0 (D) 2
(9)直线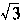 x+y-2 x+y-2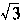 =O截圆x2+y2=4得的劣弧所对的圆心角为
(A) =O截圆x2+y2=4得的劣弧所对的圆心角为
(A)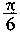 (B) (B)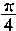 (C) (C) (D) (D)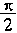 (10)如图,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,
(10)如图,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,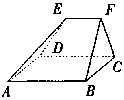 EF∥AB,EF=3/2,EF与面AC的距离为2,则该多面体的体积为
(A)9/2 (B)5 (C)6 (D)15/2
(11)若sina>tga>ctga(-
EF∥AB,EF=3/2,EF与面AC的距离为2,则该多面体的体积为
(A)9/2 (B)5 (C)6 (D)15/2
(11)若sina>tga>ctga(-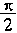 <a< <a<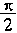 ),则a∈
(A)(- ),则a∈
(A)(-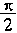 ,- ,-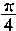 ) (B)(- ) (B)(-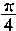 ,0) (C)(0, ,0) (C)(0,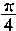 ) (D)( ) (D)(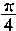 , ,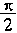 )
(12)如果圆台的上底面半径为5,下底面半径为R,中截面把圆台分为上、下两个圆台,它们的
侧面积的比为1:2,那么R=
(A)10 (B)15 (C)20 (D)25
(13)给出下列曲线:
①4x+2y-1=0 ②x2+y2=3 ③x2/2+y2=1 ④x2/2-y2=1
其中与直线r=-2x-3有交点的所有曲线是
(A)①③ (B)②④ (C) ①②③ (D)②③④
(14)某电脑用户计划使用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装
磁盘根据需要,软件至少买3片,磁盘至少买2盒则不同的选购方式共有
(A)5种 (B)6种 (C)7种 (D)8种
第II卷(非选择题共90分)
注意事项:
1.第II卷共6页,用钢笔或圆珠笔直接答在试题卷中。
2.答卷前将密封线内的项目填写清楚。
二,填空题:本大题共4小题;每小题4分,共16分,把答案填在题中横线
(15)设椭圆(x2/a2)+(y2/b2)=1(a>b>0)的右焦点为F1,右准线为l1若过F1且垂直于x轴的弦的长
等于点F1到l1的距离,则椭圆的离心率是_______
(16) 在一块并排10垄的田地中,选择2垄分别种植A,B两种作物,每种作物种植一垄,为有利于作
物生长。要求A、B两种作物的问隔不小于6垄,则不同的选垄方法共有_____种(用数字作答)
(17)若正数a、b满足ab=a+b+3,则ab的取值范围是__________
(18)α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,给出四个论断:
①m⊥n ②α⊥β ③n⊥β ④m⊥α
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:
______________________________________________________________________
三.解答题:本大题共6小题;共74分解答应写出文字说明、证明过程或演算步骤
(19)(本小题满分10分)
解方程 )
(12)如果圆台的上底面半径为5,下底面半径为R,中截面把圆台分为上、下两个圆台,它们的
侧面积的比为1:2,那么R=
(A)10 (B)15 (C)20 (D)25
(13)给出下列曲线:
①4x+2y-1=0 ②x2+y2=3 ③x2/2+y2=1 ④x2/2-y2=1
其中与直线r=-2x-3有交点的所有曲线是
(A)①③ (B)②④ (C) ①②③ (D)②③④
(14)某电脑用户计划使用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装
磁盘根据需要,软件至少买3片,磁盘至少买2盒则不同的选购方式共有
(A)5种 (B)6种 (C)7种 (D)8种
第II卷(非选择题共90分)
注意事项:
1.第II卷共6页,用钢笔或圆珠笔直接答在试题卷中。
2.答卷前将密封线内的项目填写清楚。
二,填空题:本大题共4小题;每小题4分,共16分,把答案填在题中横线
(15)设椭圆(x2/a2)+(y2/b2)=1(a>b>0)的右焦点为F1,右准线为l1若过F1且垂直于x轴的弦的长
等于点F1到l1的距离,则椭圆的离心率是_______
(16) 在一块并排10垄的田地中,选择2垄分别种植A,B两种作物,每种作物种植一垄,为有利于作
物生长。要求A、B两种作物的问隔不小于6垄,则不同的选垄方法共有_____种(用数字作答)
(17)若正数a、b满足ab=a+b+3,则ab的取值范围是__________
(18)α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,给出四个论断:
①m⊥n ②α⊥β ③n⊥β ④m⊥α
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:
______________________________________________________________________
三.解答题:本大题共6小题;共74分解答应写出文字说明、证明过程或演算步骤
(19)(本小题满分10分)
解方程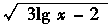 -3lgx+4=0
(20)(本小题满分12分)
数列{an}的前n项和记为Sn,已知an=5Sn-3(n∈N)求 -3lgx+4=0
(20)(本小题满分12分)
数列{an}的前n项和记为Sn,已知an=5Sn-3(n∈N)求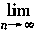 (al+a3+…+a2n-1)的值。
(21)(本小题满分12分)
设复数z=3cosθ+isinθ.求函数y=tg(θ-argz)(0<θ<)的最大值以及对应的θ值
(22)(本小题满分12分〕
如图,已知正四棱柱ABCD―A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所
成的角为45°,AB=a
(Ⅰ)求截画EAC的面积;
(Ⅱ)求异面直线A1B1与AC之间的距离;
(Ⅲ〕求三棱B1―EAC的体积。
(23)(本小题满分14分)
下图为一台冷轧机的示意图。冷轧机由若干对轧辊组成,带钢从一端输入,经过各对轧辊逐步
减薄后输出。 (al+a3+…+a2n-1)的值。
(21)(本小题满分12分)
设复数z=3cosθ+isinθ.求函数y=tg(θ-argz)(0<θ<)的最大值以及对应的θ值
(22)(本小题满分12分〕
如图,已知正四棱柱ABCD―A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所
成的角为45°,AB=a
(Ⅰ)求截画EAC的面积;
(Ⅱ)求异面直线A1B1与AC之间的距离;
(Ⅲ〕求三棱B1―EAC的体积。
(23)(本小题满分14分)
下图为一台冷轧机的示意图。冷轧机由若干对轧辊组成,带钢从一端输入,经过各对轧辊逐步
减薄后输出。
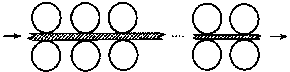 (1)输入带钢的厚度为a,输出带钢的厚度为β,若每对轧辊的减薄率不超过r0,问冷轧机至少需
要安装多少对轧辊?
(1)输入带钢的厚度为a,输出带钢的厚度为β,若每对轧辊的减薄率不超过r0,问冷轧机至少需
要安装多少对轧辊?
 (Ⅱ)已知一台冷轧机共有4对减薄率为20%的轧辊,所有轧辊周长均为1600mm,若第k对轧辊有缺陷,
每滚动一周在带钢上压出一个疵点,在冷轧机输出的带钢上,疵点的间距为Lk,为了便于检
修,请计算L1、L2、L3并填入下表(轧钢过程中,带钢宽度不变,且不考虑损耗)。
(Ⅱ)已知一台冷轧机共有4对减薄率为20%的轧辊,所有轧辊周长均为1600mm,若第k对轧辊有缺陷,
每滚动一周在带钢上压出一个疵点,在冷轧机输出的带钢上,疵点的间距为Lk,为了便于检
修,请计算L1、L2、L3并填入下表(轧钢过程中,带钢宽度不变,且不考虑损耗)。
| 轧辊序号 |
1 |
2 |
3 |
4 |
| 疵点间距Lk(单位:mm) |
|
|
|
1600 |
(24)(本小题满分14分)
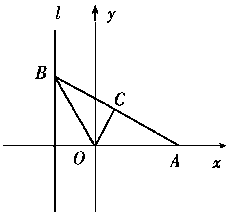
如图,给出定点A(a,0)(a>0,a≠1)和直线l:x=-LB是直线l上的动点,∠BOA的
角平分线交AB于点C,求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系。
特别说明:由于高考各方面情况的不断调整与变化,新浪网所提供的所有高考消息可能与实际情况有所出入,仅供参考。敬请考生以权威部门公布的正式信息为准。
手机短信传送天气预报、演出信息、彩票号码
文学艺术、留学移民、求职应聘、英语学习,尽在新浪网 文化教育频道。
| ![]() 北京市电信公司营业局提供网络带宽
北京市电信公司营业局提供网络带宽
 (1)如图,I是全集,M、P、S是I的3个子集,则阴影部分所表示的集合是
(A)(M∩P〕∩S (B)(M∩P)∪S
(C〕(M∩P)∩
(1)如图,I是全集,M、P、S是I的3个子集,则阴影部分所表示的集合是
(A)(M∩P〕∩S (B)(M∩P)∪S
(C〕(M∩P)∩ EF∥AB,EF=3/2,EF与面AC的距离为2,则该多面体的体积为
(A)9/2 (B)5 (C)6 (D)15/2
(11)若sina>tga>ctga(-
EF∥AB,EF=3/2,EF与面AC的距离为2,则该多面体的体积为
(A)9/2 (B)5 (C)6 (D)15/2
(11)若sina>tga>ctga(-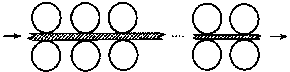 (1)输入带钢的厚度为a,输出带钢的厚度为β,若每对轧辊的减薄率不超过r0,问冷轧机至少需
要安装多少对轧辊?
(1)输入带钢的厚度为a,输出带钢的厚度为β,若每对轧辊的减薄率不超过r0,问冷轧机至少需
要安装多少对轧辊?
