说明:
一、本解答指出了每题要考查的主要知识和能力,并给了一种或几种解法供参考,如果考生的解法
与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则。
二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难,
可视影响的程度决定后继部分的给分,但不得超过该部分解答应得分数的一半;如果后继部分的解
答有较严重的错误,就不再给分。
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数。
四、只给整数分数,选择题和填空题不给中间分。
一. 选择题:本题考查基本知识和基本运算。第(1)-第(10)题每小题4分,第(11)-(14)
题每小题5分,满分60分。
(1) C (2〕A (3〕A (4) C (5)B
(6)B (7)D (8) A (9)C (10)D
(11)B (12)D (13)D (14)C
二.填空题:本题考查基本知识和基本运算,每小题4分,满分16分
(15)1/2
(16)12
(17)[9,+∞]
(18)m⊥a, n⊥β, a⊥β==>m⊥n 或m⊥n, m⊥a,
m⊥β==>a⊥β
三.解答题
(19)本小题主要考查对数函数的性质,对数不等式、无理不等式解法等基础知识,考查分类
论的思想,满分10分
解:原不等式等价于
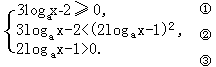 ——一一一一4
——一一一一4
由①得 logax≥2/3
由②得 logax<3/4, 或logax>1,
由③得 logax>1/2.
由此得 2/3≤logax<3/4,或logax>1.——一一一一8分
当a>1时得所求的解是 {x| ≤x< ≤x<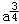 }U{x|x>a}; }U{x|x>a};
当0
{x|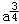 }U{x|0 }U{x|0
(20)本小题主要考查复数的基本概念、三角公式和不等式等基础知识,考查综合运用所学数
学知识解决问题的能力,满分12分。
解:由0< θ<π/ 2 得tgθ >0。
由z=3cosθ+i·2sinθ,得0<argz<π/2及tg(argz)=2sinθ/3cosθ=2/3tgθ.
故tgy=tg(θ-argz)=(tgθ-2/3tgθ)/(1+2/3tg2θ)
=1/(3/tgθ+2tgθ)
∵3/tgθ+2tgθ≥2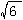
∴1/(3/tgθ+2tgθ)≤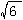 /12. /12.
当且仅当3/tgθ=2tgθ(0<θ<π/2时,即tgθ=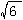 /2时,上式取等号。 /2时,上式取等号。
所以当θ=arctg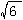 /2时,函数tgy取最大值 /2时,函数tgy取最大值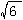 /12。 /12。
由y=-argθz得y ∈(- π/2,π/2).由于在(-π/2, π/2)内因正切函数是递增函数,函数y也
取最大值arctg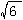 /12. 12分 /12. 12分
( 21)本小题主要考查空间线面关系、二面角和距离的概念
思维能力、空间想象能力及运算能力。满分12分。
(1)解:如图,连结DB交AC于O,连结EO。
∵底面ABCD是正方形
∴DO⊥AC。
又∵ED⊥底面AC,
∴EO⊥AC。
∴∠EOD是面EAC与底面AC所成二面角的平面角, ----2分
∴ ∠EOD=45°。
DO=(2)1/2/2a, AC=(2)1/2a, Eo=[(2)1/2a·sec45°]/2=a.
故 S△EAC=(2)1/2×a2/2 4分 |
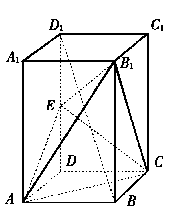 |
(II)解:由题设ABCD-A1B1C1D1是正四棱柱,得A1A⊥底面AC,
A1A⊥AC。
又 A1A⊥A1B1,
∴A1A是异面直线A1B1与AC间的公垂线。
----6分
∵D1B∥面EAC,且面D1BD与面EAC交线为EO,
∴ D1B∥EO。
又 O是DB的中点,
∴E是D1D的中点, D1B=2ED=2a。
异面直线A1B1与AC间的距离为(2)1/2a。
----8分
(III)解法一:如图,连结D1B1。
∵D1D=DB=(2)1/2a,
∴BDD1B1是正方形。
连结B1D交D1B于P,交EO于Q。
∵B1D⊥D1B。 EO∥D1B,
∴B1D⊥EO
又 AC⊥EO, AC⊥ED,
∴AC⊥面BDD1B1
∴B1D⊥AC
∴B1D⊥面EAC。
∴B1Q是三棱锥B1-EAC的高。
----10分
由DQ=PQ,得B1Q=3B1D/4=3a/2。
∴VB1-EAC=(1/3)·[(2)1/2a2/2]·(3/20=(2)1/2·a3/4.
所以三棱锥了-EAC的体积是(2)1/2·a3/4.
----12分
解法二:连结B1O,则VB1-EAC=2VA-EOB1。
∵AO⊥面BDD1B1,
∴AO是三棱锥A-EOB1的高,AO=(2)1/2·a/2
在正方形BDD1B1中,E、O分别是D1D、DB的中点(如右图),
则S△EOB1=3a2/4.
∴VB1-EAC=2×(1/30×(3a2/4)×[(2)1/2a/2}=(2)1/2·a3/4.
所以三棱锥B1-EAC的体积是(2)1/2·a3/4.----12分。 |
 |
(22)本小题主要考查等比数列,对数计算等基本知识,考查综合运用数学知识和方法解决实际问题
的能力,满分14分。
(I)解:厚度为a的带钢经过减薄率均为ro的n对轧辊后厚度为a(1-ro)n.
为使出带钢的厚度不超过β,冷轧机的轧辊数(以对为单位)应满足
a(1-ro)n≤β,
即 (1-ro)n≤β/a ----4分
由于(1-ro)n>O, β/a>0,对上式两端取对数,得
nlg(l-ro)≤lg(β/a).
由于lg(1-ro)<0,
所以n≥(lgβ-lga)/[lg(1-ro)].
因此,至少需要安装不小于(lgβ-lga)/[lg(1-ro)]的整数对轧辊
----7分
(II)解法一:第k对轧辊出口处疵点间距离为轧辊周长,在此处出口的两疵点间带钢的体积为
1600a×(1-r)k×宽度 (其中r=20%),
而在冷轧机出口处两疵点间带钢的体积为
Lk×a(1-r)4×宽度。
因宽度相等,且无损耗,由体积相等得
1600·a(1-r)k=Lk·a(1-k)4(r=20%),
即 Lk=1600·0.8K-4. ----10分
由此得 l3=2000(mm),
l2=2500(mm),
l1=3125mm)
填表如下:
| 轧辊序号K |
1 |
2 |
3 |
4 |
| 疵点间距LK(mm) |
3125 |
2500 |
2000 |
1600 |
----14分
解法二:第3对轧辊出口疵点间距为轧辊周长,在此处出口的两疵点间带钢体积与冷轧机出口处两疵点
间带钢体积相等,因宽度不变,有:
1600=L3·(1-0.2),
所以 L3=1600/0.8=2000(mm). ----10分
同理 L2=L3/0.8=2500(mm).
L1=L2/0.8=3125(mm).
填表如下:
| 轧辊序号K |
1 |
2 |
3 |
4 |
| 疵点间距LK(mm) |
3125 |
2500 |
2000 |
1600 |
----14分
( 23)本小题主要考查函数的基本概念、等比数列、数列极限的基础知识,考查归纳、推理和综
合的能力。满分14分。
(1)解:依题意f(0) =0,又由f(x1)=1, 当0≤y≤1时,,函数y=f(x)的图象是斜
率为b0=1的线段,故由
f(x1)-f(0)/x1-0=1 得x1=1 2分
又由f(x2)=2,当1≤y<2时,函数y=f(x)的图象是斜率为B的线段,故由
f(x2)-f(x1)/X2-X1=b 即x2=1+1/b.2分
记x0=0,由函数y=f(x)图象中第n段线段的斜率为bn-1,故得
f(xn) -f(xn-1)/xn-xn-1=bn-1,
又f(xn)=n,f(xn-1)=n一1;
∴xn-xn-1 =(1/b)n-1,n=1,2,…。
由此知数列{xn-xn-1}为等比数列,其首项为1/b,公比为1/b
因 b≠1,得
xn=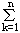 (xK-XK-1) (xK-XK-1)
=1+1/b …+1/bn-1=b-(1/b)n-1,
即 xn=b-(1/b)n-1/(b-1).——一一6分
(II)解:当0≤y≤1,从(I)可知y=x, 即当0≤x≤1时,f(x)=x
当n≤y≤n十1时,即当xn≤x≤xn+1时,由(I)可知
f(x)=n+bn(x-xn)(xn≤x≤xn+1,n=1,2,3…)——一一8分
为求函数f(x)的定义域,须对xn=b-(1/b)n-1/(b-1)(n=1,2,3…)进行讨论
当b>1时,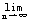 xn= xn=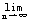 b-(1/b)n-1/(b-1)=b/(b-1) b-(1/b)n-1/(b-1)=b/(b-1)
当0<b<1时,n→∞,xn也趋向于无穷大。
综上,当b>1时,y=f(x)的定义域为[0,b/(b-1));
当0<b<1时,y=f(x)的定义域为[0,+∞] ——一一10分
(24)本小题主要考查曲线与方程,直线和圆锥曲线等基础知识,以及求动点轨迹的基本技能和综合
运用数学知识解决问题的能力。满分14分。
解法一:依题意,记B(-1,b)(b∈R),则直线OA和OB的方程分别为y=0和y=-bx,
设点C(x,y),则有0≤x
的距离公式得
|y|=|y+bx|/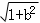 ① ----4分 ① ----4分
依题设,点C在直线AB上,故有
y=[-b/(1+a)](x-a). ----6分
由 x-a≠0,得b=-(1+a)y/(x-a). ②
将②式代入①式得
y2[1+(1+a)2y2/(x-a)2]=[y-(1+a)xy/x-a]2,
整理得
y2[(1-a)x2-2ax+(1+a)y2]=0. ----9分
若y≠0,则(1-a)x2-2as+(1+a)y2=0(0
若y=0,则 b=0,∠AOB=π,点C的坐标为(0,0),满足上式,
综上得点C的轨迹方程为
(1-a)a2-2ax+(1+A)y2=0(0≠x
∵a≠1,
∴[x-a/(1-a)]2/[a/(1-a)]2+y2/[a2/(1-a2)]=1(0≤x
由此知,当〔」「工时,方程③ 表示椭圆孤段;
当a>1时,方程③ 表示双曲线一支的弧段。
----14分
解法二:如图,设D是l与x轴的交点,过点C作CE⊥x轴,E是垂足。
(1)当|BD|≠0时,设点C(x,y),则0
由CE∥BD得 |BD|=|CE|·|DA|/|EA|=|y|/a-x(1+a).
----3分
∵∠COA=∠COB=∠COD-∠BOD=π-∠COA-∠BOD,
∴2∠COA=π-∠BOD,
∵ tg(2COA)=2tg∠COA/(1-tg2∠COA), tg(π-∠BOD)=-tg∠BOD,
tg∠COA=|y|/x, tg∠BOD = ∠|BD|/|OD|=|y|/a-x(1+a).
∴[2·|y|/x]/[1-(y2/x2)]=[|y|/(a-x)](1+a),
整理得 (1-a)x2-2ax+(1+a)y2=0(0
(II) 当|BD|=0时,∠BOA=π,则点C的坐标为(0,0),满足上式。
综合(I)(II),得点C的轨迹方程为
(1-a)x2-2ax+(1+a)y2=0(0≤x
以下同解法一。
特别说明:由于高考各方面情况的不断调整与变化,新浪网所提供的所有高考消息可能与实际情况有所出入,仅供参考。敬请考生以权威部门公布的正式信息为准。
手机短信传送天气预报、演出信息、彩票号码
文学艺术、留学移民、求职应聘、英语学习,尽在新浪网 文化教育频道。
|
![]() 北京市电信公司营业局提供网络带宽
北京市电信公司营业局提供网络带宽
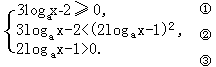 ——一一一一4
——一一一一4 ≤x<
≤x<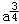 }U{x|x>a};
}U{x|x>a};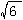

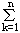 (xK-XK-1)
(xK-XK-1)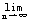 xn=
xn=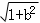 ① ----4分
① ----4分