| 江苏“高考错题”后续:教授悬赏万元求证对错 | |
|---|---|
| http://www.sina.com.cn 2004/02/19 10:29 京华时报 | |
 朱如曾教授希望用悬赏的办法证明错题真相。(本报记者 胡雪柏/摄) 对,还是错,这的确是一个问题。 去年,江苏高考中一道数学命题错误与否的争议引起许多基层数学教师和两院院士们的关注,很多人认为这是一道错题。而教育部认为此题“没有科学性错误。” 中科院力学研究所朱如曾教授则坚持认为此题为错题,他一直在行动。 2003年11月6日,朱如曾教授联系了12名院士联名公开称此题是错题,要求教育部纠错。教育部副部长袁贵仁说,教育部不怕认错。事隔3个多月,教育部考试中心称不会再对此事表态。 无奈之下,一定要对这道数学题得到个说法的朱如曾教授宣布,悬赏万元来求证此题的对错。 “江苏错题风波” 2003年6月7日,江苏高考结束后,许多考生认为数学卷第一题第1小题是道错题,向招生部门提出后,当地教育部门未予答复。一周后,南京《金陵晚报》向公众披露对该题的争议。6月17日,江苏省招办和教育部考试中心在《扬子晚报》上宣布该题“不是错题”,维持原评分标准。 当天,中科院力学研究所朱如曾教授判定“此题是错题”。6月18日,朱如曾教授向教育部考试中心据理力争未果,便向教育部周济部长建议重新组织论证。 6月23日,考试中心自己组织论证得出三点结论:题目没有科学性错误;如果题目对图形有更加清楚的说明,就不致引起争论;题目的现有形式对学生答题没有影响。 朱如曾认为,这个论证结论是自相矛盾的。随后,国内多家媒体发表报道对此结论表示质疑。5个月后,教育部考试中心一直没有明确的说法。 2003年11月6日,在朱如曾教授的联系下,郑哲敏、胡文瑞、丁伟岳、白以龙、俞鸿儒、吴承康、陈希孺、崔尔杰、张涵信、李椿萱、王崇愚和徐建中等12位两院院士,公开发表联合呼吁书,要求教育行政部门承认错误。 教育部:不是简单的对错 院士们联名表态3个多月来,朱如曾教授一直追问此事的结果。今年2月17日,记者采访了国家教育部考试中心,询问此事是否有明确的说法。 考试中心罗明主任说,朱如曾的论证有一定的道理,但并不能说这道题一定是错题。“数学上有些东西界限是模糊的。”罗明打比方说,现实中的人就不像电影中的好人与坏人,界限那么明显。他说这道题不能简单地说对或说错,而是处于“灰色地带”,比较模糊。 对朱如曾引用华罗庚的名言“数学是最容易辨别是非的”,罗明认为这个观点当年是对的,但用在这道题上又不完全对。 12名院士联名发表呼吁书后,考试中心再次论证过,“很多院士想出来跟朱如曾辩论,但考试中心一直压着。”罗明称中国数学协会看完题后说,不说话就是最好的态度。“在这道题上,朱如曾可以有不同意见,但不能强加于别人。” 罗明表示,教育部考试中心以前也曾很好地处理过错题事件,但不会再对此题表态。“该处理就处理,不该处理就不处理。” 教授无奈悬赏求证 对于教育部不再表态的做法,朱如曾教授观点一如既往:“有瑕疵就是错嘛!”他说,在数学上不应该有灰色地带。 “现在看来让教育部考试中心认错,几乎是不可能的了。”在等待数月后,朱如曾非常失望。 无奈,朱如曾教授决定通过重金悬赏的方法,向民间求证这道高考题的对错。 “谁能第一个证明这道题‘不是错题’,我重奖一万元。”朱如曾教授说,如果最后无人能获奖,没人能证出他的论证有错,则意味着公众认为此题确是错题。他希望有人能反驳他的观点,论证出这道题为什么没有错,让大家评析。 对于这次悬赏的目的,朱如曾教授说:“是求真务实,维护高考的严肃性和社会的公正性。” 据了解,奖金将由中国科学院力学研究所丹迪自动化系统工程公司提供,朱如曾教授强调说,欢迎教育部考试中心的数学命题专家、论证此题无错的专家来竞奖。 组织此次民间论证,朱如曾很谨慎,奖金从最初预备的100万降到了1万,朱教授表示是避炒作之嫌,“这件事的意义远大于金钱本身。” 朱如曾跟评奖组的专家几次商讨并确定了评奖标准,“任何人只要能正确地完成三项工作:证明该题不是错题;正确地指出我关于该题是错题的证明中所存在的关键错误;证明当初对此题坚持原评分标准比当初撤消该题的计分资格更为合理,便可获奖。” 为减少无效投稿,悬赏人同时规定,投稿者的论证须得到二位高中高级数学教师,或一位高中特级数学教师,或一位大学数学教授,或一位中科院/工程院院士的签字认同(如果证明者本人具有数学专业职称,则可以顶替一名相应职称的认同者),均可将三部分论证连同认同签字投寄北京市中关村中国科学院力学所朱如曾收(邮编:100080)。 详细情况投稿者可以直接与朱如曾教授联系,邮箱:zhurz@lnm.imech.ac.cn、电话:(010)62638533 这次民间悬赏截止到2004年4月15日,5月31日前出评奖结果。 “如果三部分证明确实都正确,最先投稿的作者为获奖者;否则不予录取,且不受理复议,若原证明者不服,可按诉讼程序以评审不公为由,向人民法院起诉。” “如果最后无一人获奖,则向公众证明该题为错题。”朱如曾教授说。 对于所做的一切,朱如曾说:“我只是想向公众证实,这道题的确是错的。” 附录朱如曾教授的论证 江苏数学卷第一题第1小题的错误,对答题与评分的影响以及应撤消其记分资格的理由。 1.原题 一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。 (1)如果函数y=ax2+bx+a的图像与x轴有两个交点,则点(a,b)在aOb平面上的区域(不包含边界)为 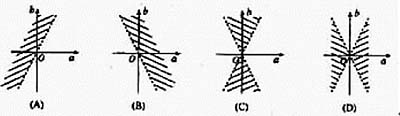 标准答案(图C)。 2.此题为错题的证明 此题的完整解是(—b—>2—a—,且a≠0)。{证明:函数y=ax2+bx+a的图像与x轴有两个交点,就是方程ax2+bx+a=0有两个不同的实根。其充分必要条件是a≠0,且b2>4a2。即(—b—>2—a—,且a≠0)。}在图A、B、C和D中,凡虚线均表示不属于区域的边界,凡相邻而不同斜率的阴影线均表示相邻而不连通的区域,这是符合惯例的。[关于区域的定义,可见《数学》,第二册(上),普通高级中学教科书,p.58: “一般地,二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧的平面区域。我们把直线画成虚线以表示区域不包括边界直线。当我们在坐标系中画不等式Ax+By+C≥0所表示的平面区域时,此区域应包括边界直线,则把边界直线画成实线。”] 然而,在标准答案图C中的b轴既未用虚线表示,并且b轴两侧与b轴相邻的角形区域又未用不同斜率的阴影线相区分,所以b轴两侧属于同一个连通区域,b轴明确地不是区域的边界。这样就使题干中“不包含边界”这个附注不含有“不包含b轴”的意思。于是图C表示了(—b—>2—a—),而不表示完整解(—b—>2—a—,且a≠0)。所以标准答案图C是错误的。此外,图A、B和D也是明显的错图。四个选项中没有一个正确,这与题干中所说“在每小题给出的四个选项中,只有一项是符合题目要求的”相矛盾,从而该题是错题!如果自相矛盾的题也可不算错题,反证法和逻辑基本规律中的“无矛盾律”岂不是就算被推翻了吗? |
| 首页 ● 新闻 ● 体育 ● 娱乐 ● 游戏 ● 邮箱 ● 搜索 ● 短信 ● 聊天 ● 点卡 ● 天气 ● 答疑 ● 交友 ● 导航 |
| 新浪首页 > 新浪教育 > 考试中心 > 正文 |
|
| 新 闻 查 询 |
|
|
|
文化教育意见反馈留言板电话:010-62630930-5178 欢迎批评指正
新浪简介 | About Sina | 广告服务 | 招聘信息 | 网站律师 | SINA English | 产品答疑
Copyright © 1996 - 2004 SINA Inc. All Rights Reserved
版权所有 新浪网![]() 北京市通信公司提供网络带宽
北京市通信公司提供网络带宽




