1.一只平底锅上最多只能煎两张饼，用它煎1张饼需要2分钟(正面、反面各1分钟)。问：煎2009张饼需几分钟？ 

　　A.2008           B.2009                 C.4016               D.4018

　　2.一个工厂有7个车间，分散在一条环形铁路上，三列火车循环运输产品。每个车间装卸货物所需工人数为25、18、27、10、20、15、30。若改为部分工人跟车，部分工人固定在车间，那么一共安排多少名装卸工可以保证各车间的装卸需求？

　　A.80              B.82              C.102            D.104

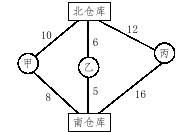
　　3.北仓库有货物35吨，南仓库有货物25吨，需要运到甲、乙、丙三个工厂中。其中甲工厂需要28吨，乙工厂需要12吨，丙工厂需要20吨。两个仓库与各工厂之间的距离如图中数字所示(单位：公里)。已知运输每吨货物1公里的费用是1元，则将货物按要求运入各工厂的最少费用是多少元？

　　A.530      B.542           C.554       D.582

　　4.某个产品由A、B、C三个部件组成，一个工人每天可以生产5个A，或者3个B，或者6个C，要使工厂每天生产的产品尽量多，该厂的210名工人全力赶工，每天最多生产多少个产品？

　　A.600           B.500          C.400           D.300

　　5.有四个人在晚上要过桥，此桥每次只能让2个人同时通过。过桥的人必须要用手电筒，而只有一个手电筒。4个人的行走速度不同：小强用1分钟就可以过桥，中强要2分钟，大强要5分钟，最慢的太强需要10分钟。请问：4个人最少需要多少分钟全部过河？

　　A.32          B.18        C.17              D.16

　　6.一个工厂有7个车间，分散在一条环形铁路上，三列火车循环运输产品。每个车间装卸货物所需工人数为25、18、27、10、20、15、30。若改为部分工人跟车，部分工人固定在车间，那么一共安排多少名装卸工可以保证各车间的装卸需求？

　　A.80             B.82               C.102         D.104

　　8.有17根11.1米长的钢管，要截成1.0米和0.7米的甲、乙两种长度的管子，要求截成的甲、乙两种管子的数量一样多。问：最多能截出甲、乙两种管子各多少根？

　　A.99       B.111        C.121         D.132

　　9.某市直机关甲、乙、丙三个系统举行春季长跑比赛，共设三个比赛项目，规定每个项目的前四名得分是：第一名5分，第二名3分，第三名2分，第四名1分。比赛结果甲机关得名次人数最少，总分却是第一；乙机关比甲机关少1分，名列第二；丙机关得名次人数最多，总分却比乙机关少1分，名列第三。请问，甲机关得了几个什么名次？

　　A。两个第一、一个第三                  B。两个第二、一个第一

　　C。一个第一、两个第三                  D。两个第一、一个第二

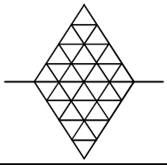
　　10.下图中心线上半部与下半部都是由3个红色小三角形，5个蓝色小三角形与8个白色小三角形所组成。当把上半图沿着中心线往下折叠时，有2对红色小三角形重合，3对蓝色小三角形重合，以及有2对红色与白色小三角形重合，试问有多少对白色小三角形重合？

　　A.4              B.5              C.6              D.7

　　参考答案：

　　1.【答案】B。中公解析：由初阶中的例题可知，煎1、2、3个饼分别需要2、2、3分钟。继续往下分析，煎4个饼最少需要4分钟，煎5个饼需要5分钟，煎6个饼需要6分钟，煎7个饼需要7分钟……煎2009个饼至少需要2009分钟。

　　2.【答案】B。中公解析：货物装卸问题。有三列火车，根据结论，所需人数应为需要人数最多的三个车间之和，即为30+27+25=82人。

　　3.【答案】B。中公解析：调运问题，通过分析将题目给的图形先转化为表(1)，

　　(1)                                   (2)

　　观察上表各列两数之差，最大的是第三列，因此北仓库的货物尽可能的供应丙工厂，即北仓库供应丙20吨。

　　在剩下的两列中，第一列的差大于第二列的差，所以南仓库的货物尽可能的供应甲工厂，即南仓库供应甲25吨。

　　因为南仓库货物分配完，甲还需要的28-25=3吨由北仓库供应，即北仓库供给丙后剩下的15吨货物中的3吨给甲，剩下的12吨给乙(如表2所示)。

　　相应的运费为3×10+25×8+12×6+20×12=542元。

　　4.【答案】D。中公解析：3、5、6的最小公倍数是30。假设同时生产30个A、B、C，生产A需要6个工人，生产B需10人，生产C需5人，一共需要6+10+5=21人，现在该厂有210人，故最多可生产30×(210÷21)=300个产品。

　　5.【答案】C。中公解析：利用过河问题的一般原则，可作如下安排：

　　小强和中强先过桥，用2分钟；再由小强把电筒送过去，用1分钟；然后由大强跟太强一起过桥，用10分钟，过去以后叫中强把电筒送回用2分钟；最后小强与中强一起过河再用2分钟，他们一共用2+1+10+2+2=17分钟全部过河。

　　6.【答案】B。中公解析：货物装卸问题。有三列火车，根据结论，所需人数应为需要人数最多的三个车间之和，即为30+27+25=82人。

　　8.【答案】B。中公解析：要想尽量多地截出甲、乙两种管子，残料应当尽量少。一根钢管全部截成1.0米的，余下0.1米，全部截成0.7米的，余下0.6米。如果这样截，再要求甲、乙管数量相等，那么残料较多。怎样才能减少残料，甚至无残料呢？我们可以将1.0米的和0.7米的在一根钢管上搭配着截。

　　所得残料长度见下表：

　　由上表看出，方法3和方法10没有残料，如果能把这两种方法配合起来，使截出的甲、乙两种管子数量相等，那么就是残料最少的方案了。

　　设按方法3截x根钢管，按方法10截y根钢管。这样共截得甲管(9x＋2y)根，乙管(3x＋13y)根。由甲、乙管数量相等，得到9x＋2y＝3x＋13y，6x=11y。

　　由此得到x∶y=11∶6。用方法3截11根钢管，用方法10截6根钢管是符合题意的截法，共可截得甲、乙管各9×11＋2×6=111根。

　　9.【答案】A。中公解析：三个比赛项目共产生3×(5＋3＋2＋1)＝33个积分，乙机关比甲机关少1分，比丙机关多1分，则甲得12分。设甲得名次的人数为x，乙为y，丙为z，则3x＜x＋y＋z＝12。所以x＜4。2个得名次的人积分最多为5+5＝10，所以甲有3人得名次。12＝5＋5＋2，则甲机关得了两个第一、一个第三，选A。

　　10.【答案】B。中公解析：小三角一共有6个红色，10个蓝色和16个白色。

　　红色：｛红＋红｝＝4红，｛红＋白｝＝2红→｛红＋蓝｝不存在

　　蓝色：｛蓝＋蓝｝＝6蓝，｛蓝＋红｝＝0蓝→｛蓝＋白｝＝4蓝

　　白色：｛白＋红｝＝2白，｛白＋蓝｝＝4白→｛白＋白｝＝10白

　　即有5对白色小三角形重合。