数学中考时的这类题 才是名副其实的验金石

　　近些年，数学中考试题中新定义题型有了一席之地。一般借助高中数学或大学数学里的基础知识定义来编题，其本身难度对于高中生或大学生来说不算什么，轻而易举，但对于初中毕业生来说，就因人而异了，思维敏捷活跃的同学，可提笔解答，思路较窄应变能力不强的同学，可能就会产生不识庐山真面目的迷茫，找不到头绪。

　　其实这类题目，对于广大学子来说，是名副其实的试金石。老师平时一般没讲过，大家都是同一起跑线，考查的就是理解接受能力，新事物，看你能不能抓住它的定义内涵；考查运用能力，学以致用，现学现卖，拿过来直接解决问题，知识点与题目相结合。最能检验学生的思维逻辑能力，可以说，这类题，才是名副其实的试金石。下面通过部分中考原题大家来体验一下。

聊城市2018年中考原题。

　　上图是聊城市2018年中考数学试卷中的第12题。思路解析如下：

　　把[x ]=2x —1代入不等式[x ]≤x <[x ]+1，

　　得2x —1≤x ，x <2x —1+1，

　　解得0<x ≤1。

　　当x =1时，[x ]=2x —1=1，解得x =1；

　　当0<x <1时，[x ]=2x —1=0，解得x =1/2。

　　综上所述，答案为1或1/2。

　　无独有偶，下图是滨州市2018年中考数学试卷第12题，与上一题类型相似，同学们可以进行巩固练习，答案在图下方。

滨州市2018年中考原题。

　　答案：A。

　　提示：借助新定义的运用，根据图像性质使用排除法比较简便。

菏泽市2018年中考原题。

　　上图是菏泽市2018年中考数学试卷第7题，关于向量的新定义考查。此题虽说有点抽象，但胜在可直接套用公式，反而是典型的“纸老虎”风格，但凡能够理解题意的同学，一般属于白送分的题。

　　这道题不做讲解，其答案：A。

　　聪明的你做对了吗？

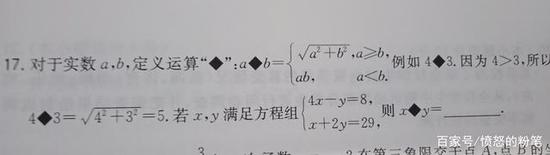德州市2018年中考原题。

　　这道题是德州2018年中考数学试卷第17题，是特殊符号运算题，也是同学们平时做练习题中常见的一种方式，按照例题依葫芦画瓢，便可迎刃而解。

　　本题答案：60。

济南市2018年中考原题。

　　济南市2018年中考数学试卷第12题，这是堪比压轴题难度的一道题。考查二次函数图像性质、解不等式组，还有数形结合思想，多数同学遇到这类题，才迎来真正的考验。

　　思路解析：

　　根据题意，把二次函数变形

　　y =mx ^2—4mx +4m —2=m （x —2）^2—2，

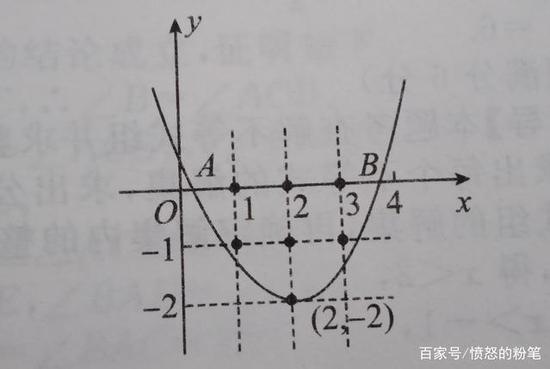
　　可得抛物线顶点坐标为（2，—2），如下图。

　　线段AB 与抛物线围成的图形中有7个整点，

　　则点A 的横坐标在0~1之间，

　　点B 的横坐标在3~4之间。（后面的步骤对于部分同学来说不太好理解，请注意图形结合）

　　①当x =0时，y >0，即4m —2>0；

　　②当x =1时，—2<y ≤—1，即—2<m —4m +4m —2≤—1；

　　③当x =3时，—2<y ≤—1，即—2<9m —12m +4m —2≤—1；

　　④当x =4时，y >0，即16m —16m +4m —2>0。

　　解不等式组，得1/2<m ≤1。

　　故选B。

　　做新定义题型，应注意以下几点：

　　1。正确理解新定义的含义，不要曲解或偏解。这个理解能力，在平时学新课或自己做新题型时可以逐渐提高；

　　2。研究例题。多数新定义题型都有小例题或公式，这是帮助学生理解题意和解决问题的关键部分。借助例题，能进一步加深对问题的了解，增强对新知识的运用能力。

　　3。调动熟悉的数学思维，巧妙结合。即使是新定义问题，整体解题思路里还是初中数学思维占据的比例大，所以把问题朝熟悉的思维方向引导，积极调动相应的知识点和思路，解决问题。

如图。

　　来源：愤怒的粉笔

　　责任编辑：陈熙