很多人因这个冷门考点错失中考 如何避免？

　　我们认真研究和分析近几年全国各地的中考数学试卷，你会发现，除了一些像函数综合问题等常见问题之外，还隐藏着一些“冷门热点”。

　　为什么叫“冷门热点”呢？此类问题看上去似乎没有那么重要，但经常又会被命题老师看中，成为考点，如像圆这一块知识是很多考生容易忽视的知识内容，但它仍是全国很多地方中考数学喜欢考查的对象。

　　对于圆这一块知识内容，在复习期间，我们一定要及时关注直线和圆的位置关系，它是学习圆的重中之重。

　　一般情况下，中考考查直线和圆的位置关系会包括以下这些知识点：

　　直线和圆的三种位置关系；

　　切线的性质和判定；

　　三角形内切圆；

　　切线长等相关知识点。

　　直线和圆有三种位置关系，具体如下：

　　1。相交：直线和圆有两个公共点时，叫做直线和圆相交，这时直线叫做圆的割线，公共点叫做交点；

　　2。相切：直线和圆有唯一公共点时，叫做直线和圆相切，这时直线叫做圆的切线；

　　3。相离：直线和圆没有公共点时，叫做直线和圆相离。

　　直线和圆的位置关系，讲解分析1：

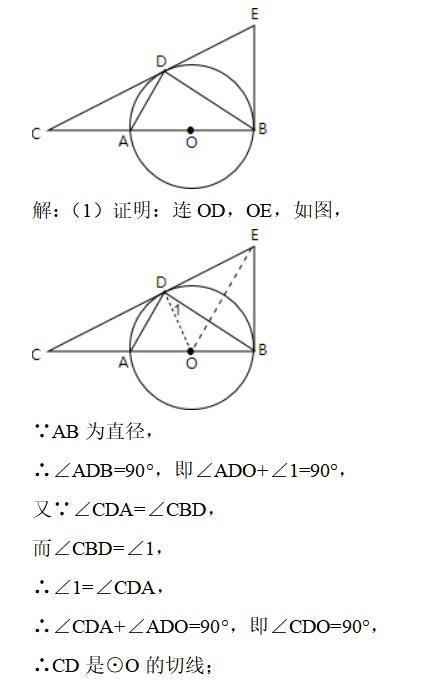
　　如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD。

　　（1）求证：CD是⊙O的切线；

　　（2）过点B作⊙O的切线交CD的延长线于点E，若BC=6，tan∠CDA=2/3，求BE的长。

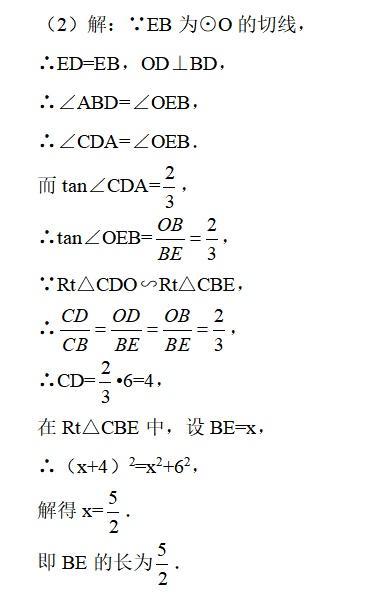
　　考点分析：

　　切线的判定与性质；圆周角定理；相似三角形的判定与性质；计算题。

　　题干分析：

　　（1）连OD，OE，根据圆周角定理得到∠ADO+∠1=90°，而∠CDA=∠CBD，∠CBD=∠1，于是∠CDA+∠ADO=90°；

　　（2）根据切线的性质得到ED=EB，OD⊥BD，则∠ABD=∠OEB，得到tan∠CDA=tan∠OEB=OB/BE=2/3，易证Rt△CDO∽Rt△CBE，得到CD/CB=OD/BE=OB/BE=2/3，求得CD，然后在Rt△CBE中，运用勾股定理可计算出BE的长。

　　解题反思：

　　本题考查了切线的判定与性质：过半径的外端点与半径垂直的直线是圆的切线；也考查了圆周角定理的推论以及三角形相似的判定与性质。

　　设⊙O的半径为r，圆心到直线的距离为d，其中直线与圆相切，除上述d=r的判定外，还有切线的判定定理：经过半径的外端，并且垂直于这条半径的直线是圆的切线。

　　直线和圆的位置关系，讲解分析2：

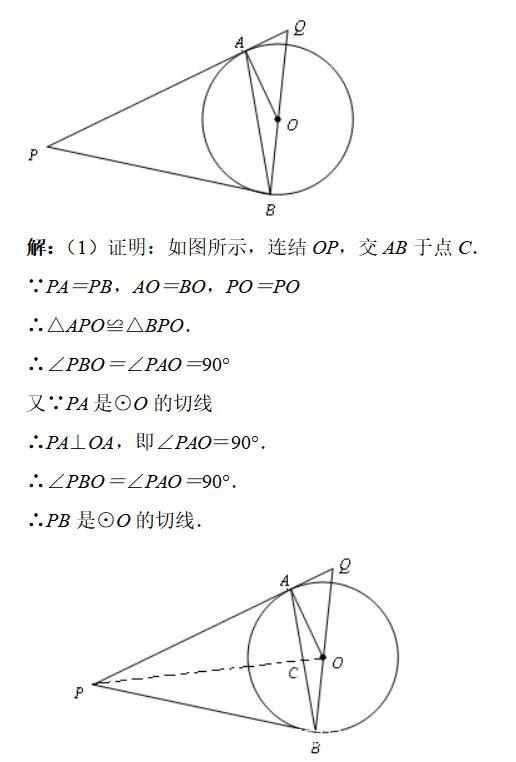
　　如图所示。P是⊙O外一点。PA是⊙O的切线。A是切点。B是⊙O上一点。且PA=PB，连接AO、BO、AB，并延长BO与切线PA相交于点Q。

　　（1）求证：PB是⊙O的切线；

　　（2）求证： AQPQ= OQBQ；

　　（3）设∠AOQ=α。若cosα=4/5.OQ= 15。求AB的长

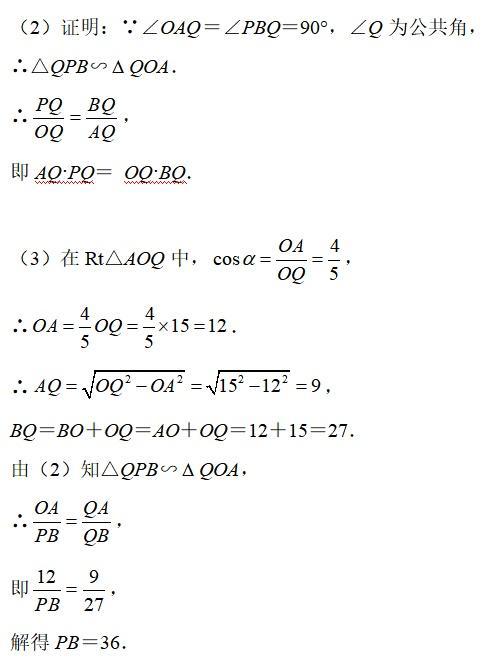
　　考点分析：

　　直线与圆的位置关系，切线，切线长，相似，解直角三角形，综合题；圆、相似

　　题干分析：

　　（1）要证PB是⊙O的切线，只要证明∠PBO=90°即可，根据已知条件可考虑连接PO，通过证明△APO≌△BPO来说明∠PBO=∠PAO=90°。

　　（2）要证明AQPQ= OQBQ，只需证明PQ/OQ=BQ/AQ即可，为此需要证明△QPB∽△QOA。

　　（3）根据已知条件解Rt△AOQ可得AQ与OA的长，则BQ的长可求，利用（2）中证得的△QPB∽△QOA，根据相似三角形的性质可求得PB的长，利用勾股定理可得PO的长，在Rt△AOB中，利用面积等积式可求得AB的一半的长，则AB的长可知。

　　解题反思：

　　（1）要证明一条直线是圆的切线，如果在已知条件中已知直线和圆已有一个公共点，那么常连接这个公共点和圆心（本题中OB已连接），再说明这条半径和直线垂直，简称“连半径证垂直”。

　　（2）等积式的证明经常需转化成比例式来证明，而证明比例式成立的首选方法是利用相似，根据相似三角形对应边成比例的性质建立比例式。

　　（3）在直角三角形中，经常利用面积等积式来求有关线段的长。

　　另外，本题前两问比较简单，易于寻找解题思路，而第（3）问综合性巧强，用到的知识较多，所要求的线段的长较多，许多同学会不能顺利做解。

　　直线和圆的位置关系，讲解分析3：

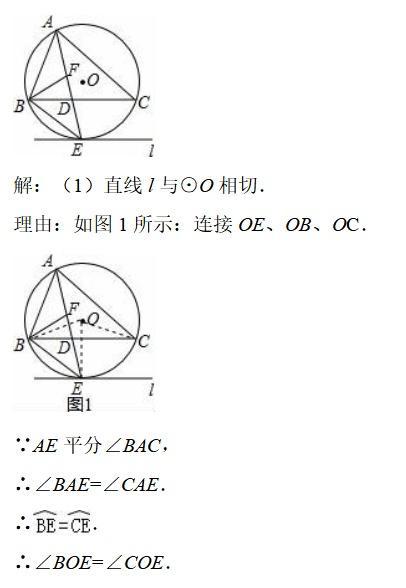
　　如图，⊙O是△ABC的外接圆，AE平分∠BAC交⊙O于点E，交BC于点D，过点E做直线l∥BC。

　　（1）判断直线l与⊙O的位置关系，并说明理由；

　　（2）若∠ABC的平分线BF交AD于点F，求证：BE=EF；

　　（3）在（2）的条件下，若DE=4，DF=3，求AF的长。

　　考点分析：

　　圆的综合题。

　　题干分析：

　　（1）连接OE、OB、OC。由题意可证明弧BE=弧CE，于是得到∠BOE=∠COE，由等腰三角形三线合一的性质可证明OE⊥BC，于是可证明OE⊥l，故此可证明直线l与⊙O相切；

　　（2）先由角平分线的定义可知∠ABF=∠CBF，然后再证明∠CBE=∠BAF，于是可得到∠EBF=∠EFB，最后依据等角对等边证明BE=EF即可；

　　（3）先求得BE的长，然后证明△BED∽△AEB，由相似三角形的性质可求得AE的长，于是可得到AF的长。

　　解题反思：

　　本题主要考查的是圆的性质、相似三角形的性质和判定、等腰三角形的性质、三角形外角的性质、切线的判定，证得∠EBF=∠EFB是解题的关键。

　　学习数学最主要的目的之一就是学会利用相关数学知识，把具体的问题变成数学模型，并对模型求解。如跟圆有关的相关几何综合问题，我们要学会利用性质定理，如直线与圆的位置关系，找到解题的关键，同时要注意数形结合、分类讨论等数学思想方法的运用。

　　来源：吴国平数学教育

　　责任编辑：陈熙