考研专硕MPAcc逻辑部分之差等关系解析
在传统逻辑方阵图中,差等关系主要指的全称和特称之间。比如所有的同学都是北京人和有的同学是北京人。这两句话之间的差等关系。有了前面的上反对关系,下反对关系和矛盾关系,我们把整个逻辑方阵图绘制成如下图形。有了这个就可以对整个逻辑精神中,关于对当关系的推理就比较齐全了。
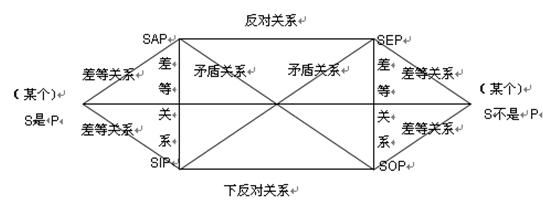 专硕MPAcc逻辑部分之差等关系
专硕MPAcc逻辑部分之差等关系在这个图上,这里必须说明的是,单称肯定和单称否定也是考试中经常遇到的,大家首先记住两个要点:一个要点是单称肯定和单称否定之间是矛盾关系。这个很好理解。举个例子来看,比如,小明是个疯子,和小明不是个疯子。这两个判断就是矛盾关系,也就是说小明要么是疯子,要么不是疯子。只能有一个真。另外一个要点是单称肯定和特称肯定之间是差等关系。这个不能用常规的生活习惯来思考。我们习惯于从全部,到有的,在到单个的。
事实上,从有的再到单个的推理不一定成立。举个例子。我们班有的同学喜欢英语,小明是我们班的,推出小明喜欢英语。这个推理是不正确的。因为我们并不知道,小明的范围是在会英语的中间还是不会英语的中间。但是反过来,若是说小明喜欢英语,小明是我们班的,必然可以推出我们班有的同学喜欢英语。这个就是我们的思维习惯与逻辑本身的差距。同学们千万要小心。虽然MPAcc逻辑考试并不考逻辑学的专门知识,但对当关系以及复合判断的推理这两个知识点在考试中还是能直接用到,如果能熟练掌握这两个知识点,对提高解题的速度和正确性还是非常有帮助的。事实上,这个图中全称和单称,全称和特称,单称和特称之间都是差等关系。从图上看,就是左右两个三角形,从上往下看,都是差等关系。
为了简洁起见,我们把模态中的必然实然和可能关系由于和所有某个和有的的关系一直,我们经常把这几个差等关系用如下推理式让大家熟记:
所有→某个→有的
必然→实然→可能
这个推理可以这样来理解,所有是包含某人和有的的,而比较容易错的是有的和某人之间的包容关系。是某人包含有的,而不是有的包含某人。我们来看几个例题。
例题1:(MPAcc2001年25题)
某仓库失窃,四个保管员因涉嫌而被传讯。四人的供述如下:
甲:我们四人都没作案。
乙:我们中有人作案。
丙:乙和丁至少有一人没作案。
丁:我没作案。
如果四人中有两人说的是真话,有两人说的是假话,则以下哪项断定成立?
A。说真话的是甲和丙。
B。说真话的是甲和丁。
C。说真话的是乙和丙。
D。说真话的是乙和丁。
E。说真话的是丙和丁。
答案:C
解析:这个题目是一个比较复杂的差等关系,和例题2和例题3不一样。首先我们把题目中的描述转换一下,甲乙二者话矛盾,丙丁依据题意必定一个真,一个假。我们用逻辑语言表达丙和丁的意思:
丙:乙和丁至少有一人没作案。 (1)¬乙∨¬丁
丁:我没作案。 (2)¬丁
根据这两句话,若(2)为真,则(1)也为真,两个真,这个是不可能的,因此,只能(2)假,这样就得到确定的信息,丁作案了并且丁说了假话。根据这个信息就知道乙一定说了真话,某个→有的,丁作案→有的人作案。故乙说了真话,因此是乙和丙说了真话,甲贺丁说了假话。故正确答案为C。
例题2:
甲、乙、丙、丁四同学在一起议论本班参加A活动的情况。
甲说:我班所有同学都参加了;
乙说:如果张帆没参加,那么李航也没参加;
丙说:李航参加了;
丁说:我班所有同学都没有参加。
已知四人中只有一人说的不正确,由此可见( )。
A。甲说的不正确,张帆没参加
B。乙说的不正确,张帆参加了
C。丙说的不正确,张帆没参加
D。丁说的不正确,张帆参加了
E。丁说的正确,张帆参加了
答案:D
解析:题眼是有个假,而四句话中正好出现了。“两个所有必有一假”,所有乙和丙说的实话。重点是当我们得知李航参加了后,马上就要知道,该班有的同学参加了为真话。这个就是用的的“某人à有的”,又因为有的同学参加了为真,它的矛盾该班所有同学都没有参加为假。故正确答案选择D。
例题3:
关于一个班的英语六级通过情况有如下陈述:
(1)班长通过了(2)该班所有人都通过了
(3)有些人通过了(4)有些人没有通过
经过详细调查,发现上述断定只有两个是正确的。可见( )。
A。该班有人通过了,但也有人没有通过
B。班长通过了
C。所有人都通过了
D。所有人都没有通过
D。该班是否有人通过没有不确定
答案:A
解析:这个题目的题眼告诉我们有两个真,两个假。根据我们所学的差等关系知道“所有à某人à有的”,在题目中就是(2)à(1)à(3)。如果假设(2)为真,那么(1)和(3)都是真的。这样出现了三个真,与题意相矛盾。故(2)比为假,(4)与(2)矛盾,故(4)为真。两真两假,去掉一真一假,还剩下的也应该是一真一假。又(1)à(3),用假设法思想,得知(1)为假,(3)为真。故答案选择A。
