作为排列组合试题的一种特殊类型，全错位排列在公考中也偶有出现。因为较之其他题型来说，全错位排列的原理需要结合举例子递推出来，故考生朋友们理解起来有一定的困难。在此京佳崔熙琳老师将考试中出现过的该类题型进行汇总，希望给各位考生提供一些帮助。

　　公考行测：数量关系之“全错位排列”经典真题剖析

　　一、全错位排列递推公式的推导

　　把编号从1到n的n个小球放到编号为从1到n的n个盒子里，假定每个盒子中的小球编号与盒子的编号不得一样(即：1号球不在1号盒，2号球不在2号盒，依次类推)，请问共有几种放法？

　　用列举法进行公式的推导：

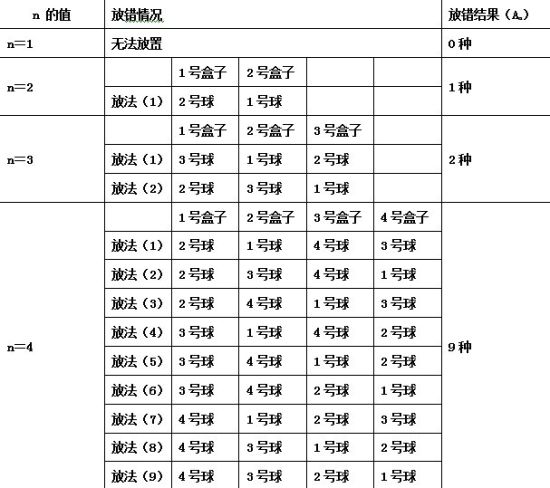图1

　　通过图1可以发现，An与n存在如下的递推关系：

　　An＝(An－2＋A n－1)×(n－1)(其中，n≥3，且A 1＝0，A 2＝1)

　　此递推公式可以产生一个全错位排列的结果数列：

　　A1＝0；

　　A2＝1；

　　A3＝(A1＋A2)×(3－1)＝2；

　　A4＝(A2＋A3)×(4－1)＝9；

　　A5＝(A3＋A4)×(5－1)＝44；

　　A6＝(A4＋A5)×(6－1)＝265..................。.

　　考生在遇到全错位排列试题时候只需要按照上述递推公式进行简单推导即可求出结果。

　　二、真题解析

　　例1：(2011年浙江省考真题55题)

　　四位厨师聚餐时各做了一道拿手菜。现在要求每个人去品尝一道菜，但不能尝自己做的那道菜。问共有几种不同的尝法？

　　A.6种              B.9种              C.12种             D.15种

　　【答案与解析】B。此题为全错位排列试题。根据全错位排列公式“An＝(An－2＋A n－1)×(n－1)(其中，n≥3，且A 1＝0，A 2＝1)”，可知，当n＝4时，共有9种尝法。

　　例2：(2010年某省考试真题)

　　五个瓶子都贴了标签，其中恰好贴错了三个，则错的可能情况共有多少种？

　　A.5                B. 10               C. 15               D. 20

　　【答案与解析】D。做此类题目时通常分为两步：第一步，从五个瓶子中选出三个，共有C(3，5)＝10种选法；第二步，将三个瓶子全部贴错，根据上表有2种贴法。则恰好贴错三个瓶子的情况有10×2＝20种。

　　京佳教育  崔熙琳

　　特别说明：由于各方面情况的不断调整与变化，新浪网所提供的所有考试信息仅供参考，敬请考生以权威部门公布的正式信息为准。