1.某公司计划购买一批灯泡，11W的普通节能灯泡耗电110度/万小时，单价20元；5W的LED灯泡耗电50度/万小时，单价110元。若两种灯泡使用寿命均为5000小时，每度电价格为0.5元。则每万小时LED灯泡的总使用成本是普通节能灯泡的多少倍？(    )

　　A.1.23 B.1.80 C.1.93 D.2.58

　　2.某商场举行周年让利活动，单件商品满300减180元，满200减100元，满100减40元；若不参加活动则打5.5折。小王买了价值360元，220元，150元的商品各一件，最少需要多少元钱？(    )

　　A.360 B.382.5 C.401.5 D.410

　　4.由1、2、3组成的没有重复数字的所有三位数之和为多少？(    )

　　A.1222 B.1232 C.1322 D.1332

　　5.河道赛道场长120米，水流速度为2米/秒，甲船速度为6米/秒，乙船速度为4米/秒。比赛进行两次往返，甲、乙同时从起点出发，先顺水航行，问多少秒后甲、乙船第二次迎面相遇？(    )

　　A.48 B.50 C.52 D.54

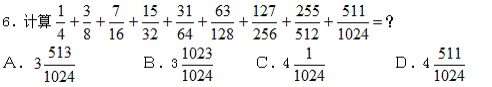
　　7.任意取一个大于50的自然数，如果它是偶数，就除以2；如果它是奇数，就将它乘3之后再加1。这样反复运算，最终结果是多少？

　　A.0 B.1 C.2 D.3

　　8.赵先生34岁，钱女士30岁，一天，他们碰上了赵先生的三个邻居，钱女士问起了他们的年龄，赵先生说：他们三人的年龄各不相同，三人的年龄之积是2450，三人的年龄之和是我俩年龄之和。问三个邻居中年龄最大的是多少岁？

　　A.42 B.45 C.49 D.50

　　9.甲乙两人从相距1350米的地方，以相同的速度相对行走，两人在出发点分别放下1个标志物，再前进10米后放下3个标志物，前进10米放下5个标志物，再前进10米放下7个标志物，以此类推。当两人相遇时，一共放下了几个标志物？

　　A.4489            B.4624 C.8978         D.9248

　　10.有4支队伍进行4项比赛，每项比赛的第一、第二、第三、第四名分别得到5、3、2、1分。每队的4项比赛得分之和算作总分，如果已知各队的总分不相同，并且A队获得了三项比赛的第一名，问总分最少的队伍最多得多少分？

　　A.7 B.8 C.9 D.10

　　参考答案及解析

　　1.【答案】D。中公解析：每万小时普通节能灯泡使用成本为20×2+110×0.5=95元；每万小时LED灯泡使用成本为110×2+50×0.5=245元。所求即为245÷95=2.58。

　　2.【答案】B。中公解析：如下表：

　　因此最少需要180+120+82.5=382.5元。

　　4.【答案】D。中公解析：对其中任何一个数字，分别有2次出现在个位，所以所有这些数字的个位数字之和是(1+2+3)×2=12，同理所有这些数字的十位、百位数字之和都是12，所以所有这些数字之和是12+12×10+12×100=1332，选择D。

　　5.【答案】C。中公解析：甲船顺水速度为2+6=8米/秒，逆水速度为6-2=4米/秒；乙船顺水速度为2+4=6米/秒，逆水速度为4-2=2米/秒。

　　第二次相遇，甲、乙共航行了4倍的赛道长度，甲航行两倍的赛道长度用时120÷8+120÷4=45秒，乙航行一倍的赛道长度用时120÷6=20秒。

　　甲顺水、乙逆水航行的时候第二次相遇，当甲恰好从起点要开始顺水行驶的时候，乙已经逆水航行了2×(45-20)=50米，则乙距起点120-50=70米，此时甲乙相遇用时70÷(8+2)=7秒，共用时45+7=52秒，选择C。

　　7.【答案】B。中公解析：此题可以用特值法，选择特殊值64，反复运算后得到最终结果为1。

　　【提示】因为原题中没有终止的机制，所以实际上此题最终的结果是4、2、1循环，我们这里选取循环中最小的数作为最佳答案。

　　8.【答案】C。中公解析：2450=2×5×5×7×7，A、B两项不是2450的因数，可以直接排除；

　　若年龄最大的为49岁，则剩余两个人的年龄之和为64-49=15，年龄之积为50，则正好一个为10岁，一个为5岁，C项满足题意；

　　若年龄最大的为50岁，则剩余两个人的年龄之和为64-50=14，年龄之积为49，此时只能两个都为7岁，这与三人年龄各不相同矛盾，排除D项。

　　9.【答案】D。中公解析：甲、乙两人以相同的速度相对行走，放下标志物的方法也是一样的，因此，两人所放的标志物总数应该是一样的，我们只需要考察其中一个人的即可。

　　甲每走10米放下一定数量的标志物，这些标志物数量构成首项为1，公差为2的等差数列。甲、乙速度相同，因此甲所走的路程为1350÷2=675米。

　　等差数列项数为[675÷10]+1=68项，则甲所放的标志物总数为1×68+68×(68-1)÷2×2=4624个。两人放的标志物总数为4624×2=9248个。

　　10.【答案】B。中公解析：4支队伍的总分为4×(5+3+2+1)=44分，其中A最少拿5×3+1=16分，即剩余三个人最多拿44-16=28分，要使总分最少的人拿最多的分，则三个人的分数要比较平均，正好8、9、11满足条件。经验证，8、9、11是可以满足条件的，因此选择B。