难倒无数英雄好汉的公务员考试行测题
1.从0、1、4、7、9中选4个数字组成若干个四位数,把其中能被3整除的四位数从小到大排列起来,那么第十个数是( )。
A.4017 B.4071 C.4107 D.4170
【答案】无答案。解析:0、1、4、7、9除以3的余数分别为0、1、1、1、0。要使该四位数能被3整除,只能去掉0或9其中一个数。四位数从小到大排列为1047、1074、1407、1470、1479、1497、1704、1740、1749、1794…,此题无答案。
【选题原因】此题无答案。
2.任意取一个大于50的自然数,如果它是偶数,就除以2;如果它是奇数,就将它乘3之后再加1。这样反复运算,最终结果是多少?
A.0 B.1 C.2 D.3
【答案】B。解析:此题可以用特值法,选择特殊值64,反复运算后得到最终结果为1。
【提示】因为原题中没有终止的机制,所以实际上此题最终的结果是4、2、1循环,我们这里选取循环中最小的数作为最佳答案。
【选题原因】此题没有终止机制,实际上最终结果是4、2、1循环,故此题不严谨。
3.某次抽奖活动在三个箱子中均放有红、黄、绿、蓝、紫、橙、白、黑8种颜色的球各一个,奖励规则如下:从三个箱子中分别摸出一个球,摸出的3个球均为红球的得一等奖,摸出的3个球中至少有一个绿球的得二等奖,摸出的3个球均为彩色球(黑、白除外)的得三等奖。那么不中奖的概率是:
A。在0~25%之间 B。在25~50%之间
C。在50~75%之间 D。在75~100%之间
3.【答案】B。解析:分析可知,要不中奖,则至少要取出一个黑球(或白球),且不能取出绿球,所有情况如下:
①一个黑球(或白球)、两个非绿的彩球,概率为C(上1下3)×2/8×5/8×5/8=150/512;
②两个黑球(或白球)、一个非绿的彩球,概率为C(上1下3)×5/8×2/8×2/8=60/512;
③三个黑球(或白球),概率为2/8×2/8×2/8=8/512;
则不中奖的概率为150/512+60/512+8/512=218/518,在25%和50%之间。
【选题原因】要想使分类不重不漏,需要考虑较多。
4.河道赛道场长120米,水流速度为2米/秒,甲船速度为6米/秒,乙船速度为4米/秒。比赛进行两次往返,甲、乙同时从起点出发,先顺水航行,问多少秒后甲、乙船第二次迎面相遇?
A.48 B.50 C.52 D.54
【答案】C。解析:甲船顺水速度为2+6=8米/秒,逆水速度为6-2=4米/秒;乙船顺水速度为2+4=6米/秒,逆水速度为4-2=2米/秒。
第二次相遇,甲、乙共航行了4倍的赛道长度,甲航行两倍的赛道长度用时120÷8+120÷4=45秒,乙航行一倍的赛道长度用时120÷6=20秒。
甲顺水、乙逆水航行的时候第二次相遇,当甲恰好从起点要开始顺水行驶的时候,乙已经逆水航行了2×(45-20)=50米,则乙距起点120-50=70米,此时甲乙相遇用时70÷(8+2)=7秒,共用时45+7=52秒,选择C。
【选题原因】两船顺流和逆流时间不同,速度不同,需分段考虑。
5.已知4/15=1/A+1/B,A、B为自然数,且A≥B,那么A有几个不同的值?
A.2 B.3 C.4 D.5
【答案】B。解析:由A≥B可知,1/A≤1/B,所以4/15=1/A+1/B≤1/B+1/B=2/B,则1/B≥2/15。又1/B≤1/A+1/B=4/15,故2/15≤1/B≤4/15,15/4≤B≤15/2,从B为自然数可知,B可以取4、5、6、7。当B=4,A=60;当B=5,A=15;当B=6,A=10;当B=7,A不为自然数,舍去。故A有3个不同的值。
【选题原因】分式计算,需用到极限思想,并需分情况讨论,难度较大。
6.小赵、小钱、小孙一起打羽毛球,每局两人比赛,另一人休息。三人约定每一局的输方下一局休息。结束时算了一下,小赵休息了2局,小钱共打了8局,小孙共打了5局。则参加第9局比赛的是:
A。小赵和小钱 B。小赵和小孙
C。小钱和小孙 D。以上皆有可能
【答案】A。解析:小赵休息了2局,则小钱和小孙打了2局;小孙共打了5局,则小孙和小赵打了5-2=3局,小钱和小赵打了8-2=6局。所以三人一共打了2+3+6=11局,由于两个人不可能连续打两局,则小钱和小赵打的6局只能是第1、3、5、7、9、11局,选择A。
【选题原因】此题需要较强的逻辑推理能力,题目讲解起来比较困难。
7.在空间中最多能放置多少个正方体,使得任意两个正方体都有一部分表面相接触?【2013-山东-56】
A.4 B.5 C.6 D.7
【答案】C。解析:在同一平面上放置立方体,要保证任意两个都有一部分表面接触,则最多只能是3个正方体。在空间中来完成这件事情,正方体最多的情况相当于是先在两个平面上各放3个两两表面接触的正方体,然后使这两个平面重合,调整两个平面中正方体的位置,使任意两个都表面接触。如下图所示:
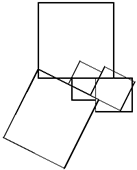
【选题原因】此题要求考生有较强的空间想象能力,不容易想出,也不容易给学生讲明白。
8.为了浇灌一个半径为10米的花坛,园艺师要在花坛里布置若干个旋转喷头,但库房里只有浇灌半径为5米的喷头,问花坛里至少要布置几个这样的喷头才能保证每个角落都能浇灌到?
A.4 B.7 C.6 D.9
【答案】B。解析:已知花坛是半径为10米的大圆,喷头是半径为5米的小圆,此题转化为求“多少个半径为r/2的小圆可以完全覆盖半径为r的大圆?”首先4个小圆的面积和恰好等于一个大圆的面积。为保证小圆尽可能的覆盖大圆,当4个小圆不重叠时,所覆盖大圆部分的面积必小于大圆自身面积。若用5个小圆覆盖大圆,因为小圆的直径等于大圆的半径,所以当5个小圆不重叠时,无法盖住大圆的圆周,而6个小圆则恰好盖住大圆圆周,此时中间空白处再加1个小圆,可将大圆完全覆盖,所以共需要7个小圆。如图所示:
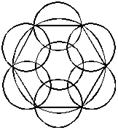
故此题选择B。
【选题原因】此题必须通过画图才能解释为什么答案选择B,且方法无法广泛使用。
9.把一个正四面体的每个表面都分成9个相同的等边三角形,用任意颜色给这些小三角形上色,要求有公共边的小三角形颜色不同,问最多有多少个小三角形颜色相同?
A.12 B.15 C.16 D.18
【答案】B。解析:
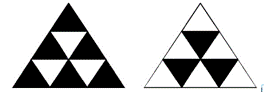
图1 图2
我们考虑小三角形颜色相同最多的那种颜色,设其为黑色。在图1中,我们将不相邻的三角形涂一种颜色,因为要求有公共边的三角形颜色不同,则黑色部分三角形的颜色一样,因此余下三个面相对于这个面的位置是一样的,我们只要分析其中的一个面即可,如图2所示,只有三个三角形能涂黑色,因此最多有6+3×3=15个小三角形颜色相同。
【选题原因】立体图形涂色,需较强的空间想象力和分析能力,题目讲解复杂。
10.学校举办一次中国象棋比赛,有10名同学参加,比赛采用单循环赛制,每名同学都要与其他9名同学比赛一局。比赛规则,每局棋胜者得2分,负者得0分,平局两人各得1分。比赛结束后,10名同学的得分各不相同,已知:
(1)比赛第一名与第二名都是一局都没有输过;
(2)前两名的得分总和比第三名多20分;
(3)第四名的得分与最后四名的得分相等;
那么,排名第五名的同学的得分是( )。
A.8 B.9 C.10 D.11
【答案】D。解析:根据题意可知,共需要进行C(上2下10)=45场比赛,每一场的总得分肯定是2分,则所有分数加在一起是45×2=90分。设第一名到第十名的得分依次为a1、a2、a3、……a10。
第一名和第二名一局都没有输过,所以第一名最多是8胜一平,即a1≤17,第二名最多是7胜2平,即a2≤16。
第三名比前两名得分和少20分,即a3=a1+a2-20,则a3≤17+16-20=13。
已知a4<a3,则有a4=a7+a8+a9+a10≤12。
已知a5<a4,则a5≤11。
已知a1+a2+a3+a4+a5+a6+a7+a8+a9+a10=90,即2(a1+a2+a4)+a5+a6=110,且a1+a2+a4≤17+16+12=45,则a5+a6≥20。
已知a5>a6,故a5>10,由上述分析可知,a5≤11,则有10<a5≤11,所以a5=11。
【选题原因】此题需要较强的分析能力,题干中的每个条件都需要分析,而且每个条件之间都有联系,需要分析出来,题目难度较大。
- 2014国考行测考前30天冲刺攻略2013-10-28 10:35
- 智商超过120才能做出的国考行测真题2013-10-28 10:24
- 2014年国考行测语言题备考“八字诀”2013-10-25 18:16
- 2014年国考行测备考:领悟言外之意2013-10-25 17:54
- 2014年国考行测数量关系考题预测2013-10-25 17:52
- 2014国考行测:判断推理模块备考指导2013-10-25 17:13
- 2014国家公务员考试行测言语理解复习思路2013-10-25 16:45
- 2014国家公务员考试行测:快速排除错误选项2013-10-25 16:19
