行测考试的工程类题中经常会考正负效率交替的合作问题，通常我们称此类题目为青蛙跳井问题。本文将通过详细讲解典型例题，为考生总结此类题目的解题技巧。

　　例：一只青蛙想从一口10米深的井中跳出，一天跳，可以跳3m，一天休息，由于井壁比较滑，会下滑1m，如此交替进行。请问这只青蛙几天能跳出这口井？

　　中公解析：在此类问题中我们知道，两天构成一个循环，一个循环的效率为+3-1=+2m，周期为两天。很多人会觉得青蛙跳出来正好需要5个循环，共计10天。但是实际上并不是，如下图所示：

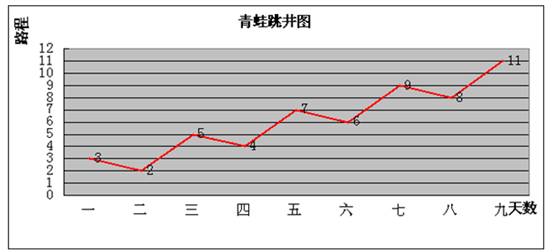
　　从图中可以看出，实际在8天多，青蛙就已经跳出这口井了。所以在做题过程中要树立一种预留思想。当青蛙经过几个整循环后只要大于10-3=7m，青蛙就能跳出去，所以我们要把3m作为预留量。首先我们要判断有多少个整循环和剩余的量，不管是均为正效率的交替合作，还是正负交替的交替合作，主要的关键在于剥离整循环和剩余量。可得：

　　2×[N]≥10-3，[N]=4

　　注：[N]为能取的最小整数

　　即经过4个整循环，剩余量10-4×2=2m

　　剩余量时间：2/3天，整循环时间：4×2=8天

　　共计：8+2/3=8.67天

　　判断有几个整循环的关键在于找预留量，实际上预留量为一个循环效率能达到的最大值，我们把这个值叫做循环效率最大增量，比如说下面这几组效率能达到循环效率最大增量为：

　　+3   +5    -7    +9       循环效率最大增量+10

　　+12  -7    +6    -7       循环效率最大增量+12

　　注：循环效率最大增量就是从第一个数字开始加，不一定全部加完，能加出的最大值。

　　综上所述，青蛙跳井问题的解题方法为：

　　(1)找一个循环量的效率和，同时计算出循环周期

　　(2)找循环效率最大增量作为预留量

　　(3)找整循环：循环量×[N]≥总量-最大增量，[ N]为满足不等式的最小正整数

　　(4) 计算整循环时间=[N]x周期

　　(5)计算剩余量=总量-循环量×[N]  

　　(6)计算剩余量时间 

　　(7)计算总时间        

　　中公教育[微博]专家提醒考生，解决青蛙跳井问题，要掌握以上方法，并加以练习，便可快速正确的解答此类问题。