解决公务员[微博]考试行测图形推理问题的关键是发现已知图形之间的内在联系与区别，只有掌握正确的解题分析方法，才能有效地观察、辨别、分析图形，做出正确的推理。下面中公教育[微博]专家就总结三种分析方法：异中求同、同中求异、特征分析，希望广大考生在运用的时候能做到相互结合、灵活运用。

　　一、异中求同

　　通常题干所给的图形都是形状各异的，此时可以通过寻找这组图形之间的共同特征，来确定图形推理规律，这种方法称为“异中求同”。

　　对图形的求同通常表现在两个方面：图形的特征属性和图形的构成元素。

　　(一)特征属性求同

　　图形的特征属性求同，即在对题干图形细致观察之后，对题干图形的特征属性加以比较，寻找它们的共同点，由此找到图形推理规律，特征属性求同应用十分广泛，在顺推型图形推理、九宫格图形推理、分类型图形推理中应用十分有效。

　　【例题1】

　　中公解析：题干图形差异较大，都有封闭区域，但在数量上不构成规律。考虑其整体特征，发现题干图形都是轴对称图形，选项中只有D 项符合，答案为D。 

　　(二)构成元素求同

　　图形的构成元素求同，即从题干图形的构成元素或组成部分出发，寻找它们的共同点，由此找到图形推理规律。

　　【例题2】

　　中公解析：第二个图形较为特殊，含有较多的线条以及交点，并形成了2 个封闭区域，观察前后两个图形，发现前一个图形含有1 个封闭区域，后一个图形含有3 个封闭区域，由此确定本题规律为图形中的封闭区域数分别为1、2、3、4、(5)，由此选择D。 

　　“异中求同”分析总结：

　　1.使用“异中求同”时应先对所给图形进行整体把握，寻找图形间外部整体特征的相同点。

　　2.使用“异中求同”时应尽可能从多个角度分析，全面考虑所有的共同点，然后结合选项得出正确答案。

　　二、同中求异

　　当题目中所给的一组图形在构成上有很多相似点或形式上表现一致，但是通过“求同”不能解决问题时，就需要发散思维，同中求异，通过对比寻找图形间的细微差别或者图形间的转化方式来解决问题。

　　(一)寻找细微差异

　　通过对比一组图形在元素的构成、排列、位置等方面的差异，确定图形推理规律。“求异”是建立在“求同”的基础上的，所以“求异”之前先应“求同”。

　　【例题1】

　　中公解析：首先整体来看题干所给出的图形的组成元素及其个数，都是由2个星星和2个三角形分布在4×4的方格中构成的，图形的构成元素相同、元素的个数也相同，图形表现出的唯一不同是这些小图形在方格内的位置不同。

　　分别来看，所有的三角形都分布在表格的边界上，所有的星星都在方格的对角线上，这样就找到了图形组成元素在位置分布上的规律，结合选项，符合这个规律的只有D项。

　　(二)寻找转化方式

　　通过对比一组图形在元素的构成、排列、位置等方面的差异，确定题干图形间的转化方式。

　　【例题2】

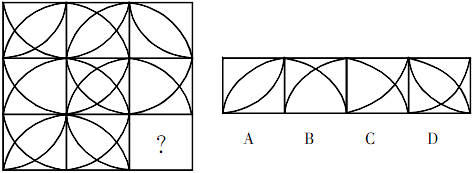
　　中公解析：这道题目在整体形式上迷惑性很大，图形整体看上去可以组成以中心的四个点为圆心的圆，如果这样考虑，会首先把B项排除，但不能找出可信的规律区分其他三个选项。

　　从图形的元素构成来看，题干图形都是由2条、3条或4条连接正方形顶点的曲线构成的，图形间最大的差异是曲线的方向。对比发现，每行三个图形中不存在完全相同的线条，每行前两个图形具有相同的线条，而且这些相同的线条在第三个图形中都不出现，据此可以确定此题的规律是每行前两个图形叠加去同存异得到第三个图形，B是正确答案。

　　“同中求异”分析总结：

　　1.使用“同中求异”时一般先对比图形的内在细节特征，然后再分析外部整体特征。

　　2.如果一组图形经过对比有多于一个的不同点，则需要对这些不同点加以比较，选择最为显著的不同点来结合选项验证。

　　三、特征分析

　　特征分析法是从题干中的典型图形、构成图形的典型元素出发，大致确定图形推理规律存在的范围，再结合其他图形及选项猜证图形推理规律的分析方法。

　　【例题】

　　中公解析：题干共五个图形，其中第二个图形是一个汉字，其他图形均为规则的线条类图形。显然，第二个图形是特殊的，从它入手。出现汉字且不全为汉字，首先考虑封闭区域数，很显然题干图形有且只有一个封闭区域，选项中只有D符合，故答案为D。

　　“特征分析”方法总结：

　　1.“特征分析”并不适用于所有的图形推理题目，有些题目中未必存在特征图形，应注意与“求同、求异”的结合使用。

　　2.“特征分析”应与排除法结合使用以提高解题速度。解题过程中，应根据特征元素之间的关系，排除某些选项。

　　中公教育专家建议考生们仔细研究以上方法，一定能加快做题速度，从而提高分数。

　　本文由中公教育供稿