一、规律探索类问题
探索规律型问题也是归纳猜想型问题,其特点是:给出一组具有某种特定关系的数、式、图形,或是给出与图形有关的操作变化过程,或某一具体的问题情境,要求通过观察分析推理,探究其中蕴含的规律,进而归纳或猜想出一般性的结论。
探索规律题一般可分为数的规律、式的规律、图形的规律或与图形有关的操作变化过程的规律等类型。此类题涉及的知识面广,可以是代数领域也可以是几何领域,主要涉及的知识是列代数式。主要思想方法是从特殊到一般的归纳猜想
典型例题:
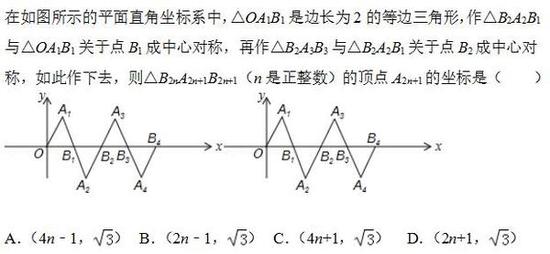


解题反思:
此题主要考查了坐标与图形变化﹣旋转问题,要熟练掌握,解答此题的关键是分别判断出An的横坐标、纵坐标各是多少。
探索规律,一般指变量的变化规律,抓住了变量,就抓住了解决问题的关键。解决此类问题的主要方法是观察、分析、归纳、验证。一般可把变量和序列号n放在一起加以比较,从而发现其中的规律。其中有的问题可转化成数字规律,有的问题的规律具有循环性,只要找到“循环节”,便可发现其规律。
二、动态综合问题
动态综合问题”题型繁多、题意创新,考察学生的分析问题、解决问题的能力,内容包括空间观念、应用意识、推理能力等,是近几年中考数学试题的一大热点和难点。动态综合问题已成为中考数学试题的热点、难点题型。这类试题以运动的点、线段、变化的角、图形的面积为基本条件,给出一个或多个变量,要求确定变量与其他量之间的函数等其他关系;或变量在一定条件为定值时,进行相关的计算和综合解答,解答这类题目,一般要根据点的运动和图形的变化过程,对其不同情况进行分类求解。
动态综合问题是一类开放性题目,解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题。
典型例题:




解题反思:
本题主要考查了勾股定理、相似三角形的判定和性质、列函数解析式、求二次函数的最值,综合性强,能根据已知条件把所需线段用含t的代数式表示来,灵活用用三角形的性质和判定是解决问题的关键,要注意分类思想、方程思想的应用。
三、数学形结合思想问题
数形结合思想是利用几何图形的性质研究数量关系或利用数量关系研究几何图形的性质,使数量关系与几何图形巧妙地结合起来,使问题得以解决的一种数学思想。数形结合思想方法的应用,可帮助我们理解题意,分清已知量、未知量,理顺题中的逻辑关系。
典型例题:



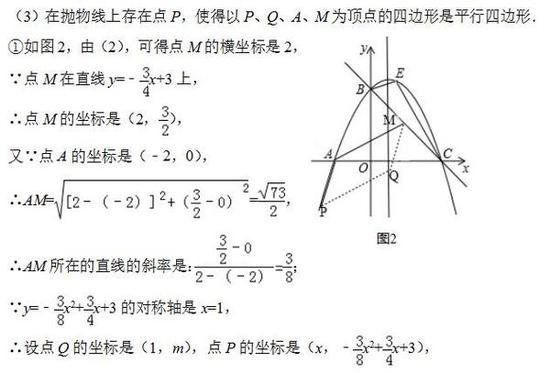
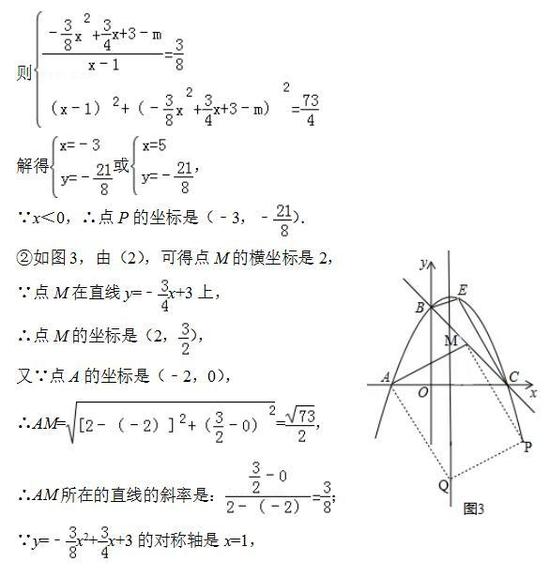


解题反思:
(1)此题主要考查了二次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力。
(2)此题还考查了函数解析式的求法,以及二次函数的最值的求法,要熟练掌握。
(3)此题还考查了三角形的面积的求法,要熟练掌握
作者:吴国平