2015广东公务员考试数量关系必考知识点
第一部分 数字推理部分
数字推理是广东省考每年必考的一种题型,每年题量为5道,数量虽少,但也不能忽视,在竞争激烈的公考路上,一分也会力压群雄,夺得武林至尊的宝座。但是许多学生看到这一类题就感到束手无策,只会简单的做差寻求答案,甚至还有学生凭借所谓的“题感”去猜蒙,完全凭运气、拼人品,久而久之,对数字推理这部分就忽视了。
(一)题型概述
鉴于此,华图教育[微博]资深老师研究近八年的考题发现,数字推理在2012年产生了一个巨大的分水岭:从难度来看,在2012年以前,数字推理部分难度可谓让人“望洋兴叹”,但是在2013年和2014年这两年来看,数字推理这个模块数字推理更侧重于基础,难度梯度有明显的过度,即从基础题型过度到提高题型,只要系统学习过的大部分考生均能在短时间内做对3道题左右;从题型分布来看,2012年之前侧重考察递推数列、多重数列、拆分组和数列、图形数列以及特殊数列,其中特殊数列就是考生常说的“变态数列”,但是在2012年之后其侧重点转移为多级数列、分数数列、多重数列、拆分组和数列,其中多级数列,这种思路比较简单、侧重基础的题型每年占据2道,其重要性不言而喻。不难发现,近八年的题型中,多重数列和拆分组和数列始终是考试的重点。那么,2015年省考有可能还会延续2013年和2014年的题型特点。接下来的复习备考中上述常考题型希望引起大家的重视。
(二)数字推理必考知识点汇总表

从图表可以发现,07年-14年期间常考的知识点为多级数列的做差、做商思想;递推数列常考知识点为递推倍思想;多重数列的交叉、分组思想;以及拆分组和数列的数字加和和数字拆裂思想。可以看出,上述的这几种思想几乎都是每年必考的知识点,也就是要求考生必须掌握的思想和技巧。
(三)高分技巧解读
从上图中我们了解到重点题型考察的思想。接下来,我们重点讲解这些思想的具体技巧。
一、多级数列:这种数列没有明显的规律。但是一般项数在5~7项。
①做差:相邻两项做差(前一项减去后一项,或者后一项减去前一项)形成的一组新数列并呈现一定的规律性。有时候,做差得不出规律,那么再次做差,即两次做差。
②做商:相邻两项相除(前一项除以后一项,或者后一项除以前一项)形成的一组新数列并呈现一定的规律性。一般情况下,相邻两项之间有明显的倍数关系时,首选考虑做商。
二、多重数列:这种数列一般项数多,一般都在7项及7项以上;或者有两个小括号。
①交叉:数列的奇数项和偶数项分别具备一定的规律,可以形成两个独立的简单数列。
②分组:分组数列通常是两两分组,即第一项和第二项一组,第三项和第四项一组,以此类推;或者第一项和最后一项一组,第二项和倒数第二项一组,以此类推,因此项数(包括未知项)一般是偶数。当项数(包括未知项)为3的倍数时,也许会出现三三分组。分组后进行组内加减乘除等运算,是分组数列的基本解题思路。
三、拆分组和数列:一般是将每一项都拆成几部分,将这几部分进行一定的运算,最后所有项体现出一定的规律。其特点:每个数字位数相等且位数较多,或者位数不等,但递增至较多位数;数字大小变化比较紊乱,能够较明显的看出变化的无规律性。
例如:abc,def,ghi,jkl,( )
①数字加和:每项的各个数字相加,即a+b+c,d+e+f,g+h+i,j+k+l,形成的新数列呈现一定的规律。或者,abc+a+b+c=def,以此类推。
②数字拆分:每个数的第一位、第二位、第三位分别成规律。即a,d,g,j成规律;b,e,h,k成规律;c,f,i,l成规律。或者a@b=c,d@e=f,以此类推。此外,还有每项的内部之间存在的规律性,例如:ab@c,de@f,gh@i,gh@l,形成的新数列呈现规律性。(注意:其中@指加减乘除。)
(四)典型例题分析
多级数列:①做差思想:
【广东-2013】6,14,22,( ),38,46
A.30 B.32
C.34 D.36
【解析】二级做差。很容易能够看出相邻数字之间的差值,即后一项减去前一项是8,是一个公差为8的等差数列,30刚好吻合,因此,本题答案为A选项。
【广东-2014】4,6,10,18,34,66,( )
A.82 B.98
C.114 D.130
【解析】二级做差。观察数列发现符合“一般来说都是整数;项与项之间相差不大;没有明显的幂次特征”,优先考虑做差,做差后发现新的数列为2,4,8,16,32,(64),为等比数列,故本题正确答案为66+64=130,选D。
②做商思想:
【广东-2013】1.8,3.6,7.2,14.4,( ),57.6
A.18.4 B.22.6
C.28.8 D.34.4
【解析】首先观察发现,相邻两项之间有明显的倍数关系,首选做商,验证发现,后一项除以前一项均为2,是一个公比为2的等比数列,故C选项符合要求。
【广东-2014】2187,729,243,81,27,( )
A.3 B.6
C.9 D.12
【解析】首先观察发现,从较小的数看起较容易,相邻两项之间有明显的倍数关系,首选做商,验证发现,前一项除以后一项均为3,是一个公比为3的等比数列,故C选项符合要求。
多重数列:①交叉
【广东-2013】3,7,9,14,27,28,81,( )
A.132 B.108
C.83 D.56
【解析】这个数列比较长,共有八项,首先考虑为多重数列。
交叉:奇数项为:3,9,27,81,偶数项为:7,14,28,( )。不难看出,奇数项单独是一个是公比为3的等比数列,偶数项单独是一个公比为2的等比数列,56与28刚好是2倍的关系。因此,本题答案为A选项。
②分组
【广东-2014】8,3,17,5,24,9,26,18,30,( )
A.22 B.25
C.33 D.36
【解析】这个数列很长,共有十项,首先考虑为多重数列。先考虑交叉,发现没有规律,无对应的答案。因为总共十项,为偶数项,考虑两两分组,发现每两项的和依次为11,22,33,44,(55=30+25),故本题正确答案为B。
【广东-2011】1,9,7,4,8,5,( ),11
A.3 B.4
C.5 D.6
【解析】这个数列比较长,共有八项,首先考虑为多重数列。先考虑交叉,发现没有规律,无对应的答案。因为总共八项,为偶数项,考虑两两分组,组内加减乘数验证后发现没什么明显规律,这时候考虑首尾分组。(1,11)(9,?)(7,5)(4,8),加和发现均为12,呈现规律,故选择A。
【广东-2012】2,2,8,-1,-2,5,1,1,2,-1,1,( )
A.-2 B.-1
C.1 D.2
【解析】这个数列很长,共有十二项,首先考虑为多重数列。先考虑交叉,发现没有规律,无对应的答案。因为总共十二项,为偶数项,考虑两两分组,组内加减乘数验证后发现没什么明显规律,又因为项数是3的倍数,考虑三三分组,即(2,2,8)(-1,-2,5)(1,1,2)(-1,1,?),发现,组内,前两个数的平方之和等于第三项,例如:22+22=8,以此类推,成立。故选择2,D选项。
拆分组和数列:①数字加和
【广东-2013】24,35,55,57,( )
A.64 B.68
C.75 D.79
【解析】依次将每个数值的两位数字相加得:6,8,10,12,(),依次推出,后面的数字加和为14,68刚好合适。因此,本题答案为B选项。
【广东-2014】768,199,827,69,904,( )
A.92 B.77
C.53 D.39
【解析】数字特征很明显不符合常规数列的特征,马上考虑数位组合,发现每项各个数位上的数字和依次为:21,19,17,15,13,(11),故本题正确答案为A。
【广东-2009】168,183,195,210,( )
A.213 B.222
C.223 D.225
【解析】数字特征很明显不符合常规数列的特征,马上考虑数位组合,发现每项各个数位上的数字和依次为:15,12,15,3,发现没什么明显规律,但是在去试探时发现:168+1+6+8=183,183+1+8+3=195,195+1+9+5=210,成立,那么,210+2+1+0=213,故选择A。
②数字拆分:
【广东-2010】1526,4769,2154,5397,( )
A.2317 B.1545
C.1469 D.5213
【解析】数字大且位数多,首先考虑数位组合,发现每项各个数位上的数字和之后没有明显规律,考虑数字拆分,发现:1526:26-15=11,4769:69-47=22,2154:54-21=33,
5397:97-53=44,呈现明显规律。故所求项为后两项减去前两项为55。C符合。
【广东-2012乡镇】5.11,6.10,7.17,8.12,( )
A.9.13 B.9.15
C.9.23 D.9.25
【解析】题目均为小数,一般情况下出现小数,或者是等比数列,或者是拆分组和数列这两种的概率是比较大。观察发现不符合等比数列的形式,考虑拆分组和数列。其规律如下:每个数的第一位为5,6,7,8,(9);小数位的规律为:2×5+1=11,2×6-2=10,2×7+3=17,2×8-4=12,即,每个数的第一位的2倍分别+1、-2、+3、-4、+5等于小数位。所以下一项为2×9+5=23。故选择C。
第二部分 数学运算
众所周知,在广东省考中,数学运算每年题量为10题,但其难度让大多考生头疼不已,更有许多考生抱着放弃的态度。所以,要想数量关系有一定的提高,仅靠短期的突击或者临场发挥是难以得到高分的。本文为大家就如何把握省考中的的重点以及必考的知识点做了详细的解说。华图教育资深老师研究近八年的考题发现,数学运算在2012年产生了一个巨大的分水岭:从难度来看,在2012年以前,数学运算部分难度比较大,但是在2013年和2014年这两年来看,数字运算基础题型有所增加,整体难度适中。从题型分布来看,2007年-2014年这几年侧重考察工程问题、行程问题、容斥原理、排列组合以及方程法思想。2015年省考有可能还会延续这八年的题型特点。接下来的复习备考中上述常考题型希望引起大家的重视。
(一)数字运算必考知识点汇总表
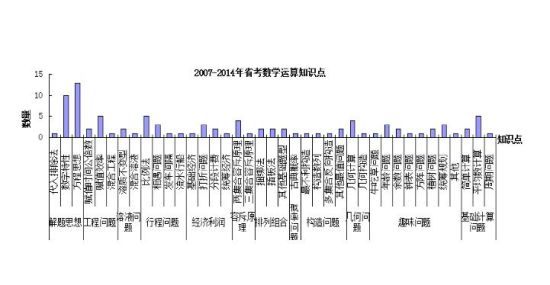
(二)高分技巧解读
从上图中我们了解到重点题型考察的思想。接下来,我们重点讲解这些思想的具体技巧。
①数字特性:包括奇偶性,即如果两个数的和为偶数那么差也为偶数,如果两个数的和为奇数,那么差也是奇数;比例倍数特性,即如果a/b=m/n,(m、n互质),那么a是m的倍数,b是n的倍数。
②方程法思想:通过找出条件中的等量关系,设未知数求出。
③赋值效率型:题目给出效率比,则赋值效率比为各自的效率;如果给出人数则赋值每个人的效率为1.
④相遇问题:相遇距离=速度和×相遇时间
(三)典型例题分析
①数字特性
【广东-2014】一些员工在某工厂车间工作,如果有4名女员工离开车间,在剩余的员工中,女员工人数占九分之五,如果有4名男员工离开车间,在剩余的员工中,男员工人数占三分之一。原来在车间工作的员工共有( )名。
A.36 B.40
C.48 D.72
【解析】根据题意设剩下的女员工x人,总人数n人。根据题意有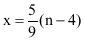 ,根据比例倍数可知,总人数减去4,是9的倍数,故本题正确答案为B。
,根据比例倍数可知,总人数减去4,是9的倍数,故本题正确答案为B。
②方程法思想
【广东-2013】某市居民用电实行分段式收费,以人为单位设定了相同的基准用电度数,家庭人均用电量超过基准用电度数的部分按照基准电费的两倍收取电费。某月,A家庭5口人用电250度,电费175元;B家庭3口人用电320度,电费275元。该市居民每人的基准用电为( )度。
A. 25 B. 30
C. 35 D. 50
【解析】假设人均基准用电为x度,基准用电电费为y元,则超过基准用电电费为2y元,依题意有: ,解得x=30,y=0.5.因此本题答案为B选项。
,解得x=30,y=0.5.因此本题答案为B选项。
③赋值效率型:
【广东-2010】有20名工人修筑一段公路,计划15天完成。动工3天后抽出5人去其他工地,其余人继续修路。如果没人工作效率不变,那么修完这段公路实际用( )
A.19天 B.18天
C.17天 D.16天
【解析】设每个人的效率为1
| 工作总量 = 工作效率 × 工作时间 | ||
| 300 | 20 | 15 |
| 60 | 20 | 3 |
| 240 | 15 | 16 |
故需要16+3=19天。
④相遇问题:
【广东-2014】一辆客车与一辆货车从东、西两个车站同时出发匀速相向而行,客车和货车的行驶速度之比为4:3。两车相遇后,客车的行驶速度减少10%,货车的行驶速度增加20%,当客车到达西车站时,货车距离东车站还有17公里。东、西两个车站的距离是( )公里。
A.59.5 B.77
C.119 D.154
【解析】根据题意令客车的行驶速度为40x,货车的行驶速度为30x,两车相遇所花的时间为t。则根据题意有 ,而总路程为(40x+30x)×t,即70xt=17*7=119公里。故本题正确答案为C。
,而总路程为(40x+30x)×t,即70xt=17*7=119公里。故本题正确答案为C。
以上的内容希望对正在备考2015广东省考的学生们有一定的启发作用。在复习备考过程中,做省考数字推理题,心态平和很重要,切忌纠结于一题之得失,要懂舍得之道。
“时不我待,只争朝夕”。准备扬帆起航向着公务员[微博]之路前进吧!最后华图教育集团预祝每位考生取得一个好成绩。
特别说明:由于各方面情况的不断调整与变化,新浪网所提供的所有考试信息仅供参考,敬请考生以权威部门公布的正式信息为准。
文章关键词: 2015广东公务员考试2015公务员考试
- 2015广东公务员考试行测理科题备考讲解2015-01-04 11:43
- 2015广东公务员考试行测技巧:解题思想2014-12-29 13:55
- 2015广东公务员考试备考三阶段2014-12-22 10:26
- 2015广东公务员考试备考战略2014-12-17 14:41
- 民进中央机关2015年考试公务员面试公告2015-02-05 14:25
- 2015江苏公务员考试申论:归纳概括能力2015-02-05 11:12

