看点 作很多孩子乘法口诀背的很熟,计算做的很溜,但对所学的概念却不理解,毕竟概念理解不是靠背诵能完成。两个孩子的“数学奶爸”夏骏轶认为,让孩子在好奇心的驱使下,陪他一起进行数学冒险,而不是刻板的死记硬背,才有助于培养他的独立思考能力,也才能让他更好地理解数学的概念。下文中,他分享实际生活经历和例题,与大家介绍了了独立思考能力该如何培养,以及如何通过“提问”,引发孩子的好奇心。
文丨夏骏轶 编辑丨李臻
一次探险引发的思考
上个周末带二宝出去逛,走过漕溪公园附近,有一排沿街商铺,台阶很高,从台阶可以走上一个挺宽的平台,如果要从平台下来,要不走前面的楼梯,要不倒退走后面的楼梯,再者就干脆从平台上跳下来。

这对于一个环境探索症重度患者的4岁男娃来说,简直就是一场美好的大冒险。平台有些高,他不敢跳,于是,他让我在平台中间等着,然后从后边楼梯爬上去,跑过平台,扒着我的脖子滑下来,往前面跑,再上楼梯,循环往复,不亦乐乎。

当我们走到街道拐角,这排商铺到了尽头,前面不再有楼梯,于是他想让我过去充当人肉梯子,我满脸坏笑说:“爸爸累了,抱不动你,你想办法自己下来。”
他有点楞神,表情好像在说:“你怎么能不按套路出牌呢?”我向他挤眉弄眼,意思是说:“小子,考验你的时候到了,快动动脑筋。”
他走到平台边看了看,想爬下来,最后还是没敢,又往后看了看,楼梯距离有些远,再往前看,因为接近拐角有两根柱子,挡住了视线,啥都看不见。我心里在默默嘀咕:“这小子到底会做什么样的选择呢?”
结果我还没来得及转念,他就往拐角方向跑过去。我在平台下面跟着他走,绕过柱子一转弯,这家伙已经跑到平台下面来了,兴冲冲的扑过来,抱住了我的腿。原来,拐过柱子,前面就有一个新的台阶。我抱起他问:“你为什么要选择往前面走啊?难道你知道前面有楼梯吗?”他一副理所当然的口气:“我不知道啊,所以才跑过去看看呗!”
一件小小的亲子事件,让我想起一个著名的心理学实验:
心理学家设置一个螺旋形栅栏。将食物放在栅栏的中心处,让一些动物从外向内寻找。由于动物沿着栅栏的通道向中心步步靠近,大多数动物都能找到食物。
但如果将动物放在栅栏的中心处,把食物放在栅栏的出口处,由于动物由内向外走的时候,看着食物忽远忽近,就搞不明白为了接近目标需要暂时远离目标,所以会在靠近食物的栅栏通道处徘徊不已,不肯“离去”,结果找不到食物。
有的时候,我们人并不比动物强多少,惯性思维使我们本能的排斥思维方式的改变,固执己见,这是一方面。但是人类有一个非常棒的天赋,就是好奇心。好奇心使得我们乐于探索世界,发现新的事物,也使得我们得以对抗旧思维,学习新方法,这是另一方面。
在之前的文章中我就谈到,要用人文视角去看儿童数学启蒙,其中有一个观点是在启蒙中发展孩子的独立思考能力,有不少家长给予反馈:孩子的思维很多时候都在原地打转,有时甚至还会倒退,独立思考很难培养。
其实,独立思考也好,数学思维也罢,建构性教学的轨迹,都不是一条直线,而是螺旋上升。很多时候远即时近,慢即是快。
学好数学,需要“远行冒险”
所谓远行,就是不走直路,走弯路。
我们在学习中,往往有一种心态——寻找捷径,致力于少走弯路。对于为了获得某种结论的学习而言,走直线自然是最经济的做法,但对于以思维培养为目标的学习,走走弯路,往往效果来的更好。
举一个小例子,现在孩子学乘法第一步做什么?背乘法口诀是吧。这和我们小时候学习区别不大,甚至和我们父辈学习乘法,也相差不远。背乘法口诀就是一条直路,它以最快的速度,帮助我们掌握乘法,但是,这是能取得最好效果的学习方法吗?不一定。
快不等于好。
很多孩子乘法口诀背的很熟,计算做的很溜,但对乘法的概念却不理解,毕竟对概念的理解不是依靠背诵能完成的。,正如远行的风景能帮助我们自然而然地,更深刻了解什么是人生一样,让孩子在好奇心的驱使下,陪着他一起进行数学冒险,才有助于培养他的独立思考能力,也才能让他更好地理解数学的概念。
以乘法的概念为例,来体验一下数学的冒险之旅。
如果让孩子做一做他们已经非常熟悉的加法:1+2+3+4+5+6+7+8+9=45,有人会说:用高斯算法很容易就算出来了。没错,但是既然是远行,就不适合用现成的方法,我们可以请孩子们画下来。
现在我们有了一个三角形,底边是9,高也是9,我们可以请孩子把这个三角形变成一个长方形吗?
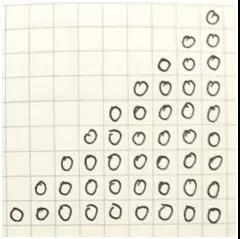
孩子们可能从来没有想过,还有这样的玩法,没有关系,这本来就是一次没有风险的冒险,想怎么玩就怎么玩,但是有一点很重要,我们需要做好一些记录,比如这样:

我们也可以提示孩子,让小石头从山顶滚下来,不管怎么样,最重要就是一家人整整齐齐,最后我们从这样的“三角形”变成了“长方形”。

好了,我们现在有了一个长方形,这下是不是很容易就数清有几块小石子了?或许有些家长很机智地发现,这其实就是5×9哈,但是别着急,既然是远行,就让我们多看一下风景,不要让旅程枯燥。
从上面的记录,我们可以和孩子一起思考:是否有些数字可以摆成一个方形,但是不是所有数字都能摆成方形呢?这样的问题引发的好奇心可以推动孩子继续探索的路边风光。
我们先拿1到10试试看,这回我们换成小方块。

有点奇怪,1、2、3这三个数好像都只能摆成这样扁扁的长方形,试试看4吧。
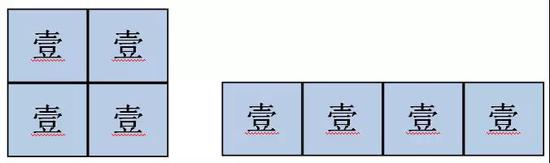
果然,4可以摆出两种样子的方形,我们可以记录下来,(2,2)和(1,4)。
之后的数字:
5有一种(1,5),
6有二种(2,3)和(1,6),
7有一种(1,7),
8有二种(2,4)和(1,8),
9有二种(3,3)和(1,9),
10有二种(2,5)和(1,10)。
11有……
依次往下,一场伟大的冒险开始了,让我们看看最后形成的“旅行地图”会是什么样的。

(为了孩子便于理解,可以用这些不同数字的方形图贴在大表格中,每个数字都尝试一下,最后就形成了“旅行地图”。)
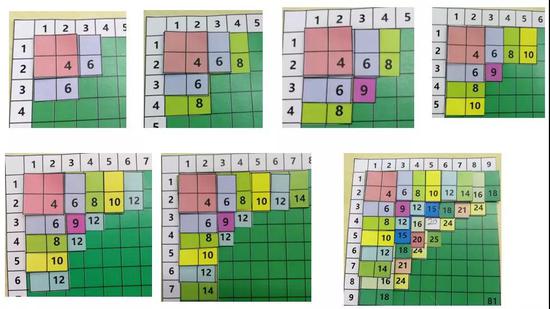
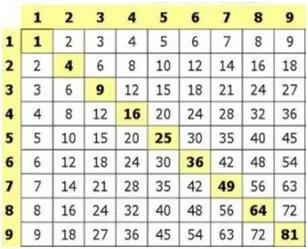
这个乘法表有别于我们常识中的99乘法表,蒙氏数学中用过,可汗学院也提到过,关键是,或许我们可能要花很长时间才能完成这次“探索旅程”,但是最后,当我们探索完1-81的数字后,回过头看我们来时的路,可能会有很多的收获:
1、理解了乘法其实就是矩形,两者可以互相转换,为以后学习图形面积奠定了基础;
2、明晰了乘法的分组概念,在这个表内任意一个数字(比如35)都能转化为一个具体的矩形,分组形态一目了然;
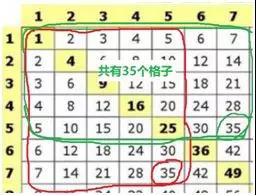
3、建立了良好的乘法模型,理解了乘法本质上是一种二维思考模式,乘法的确比加法更简便,除法与乘法是互逆的。
4、熟练了部分与整体思维,进而能帮助孩子理解数量关系应用题;
5、感知和体验了质数和因数的初步经验,对数的概念会有更深的了解。
然后,我们可以把这张表继续扩大到12×12,14×14,甚至19×19,也可以继续“远行”,比如找找表当中哪一个数字出现的次数最多,从乘法的角度理解为啥32比25大了7等等
除此以外,这样的“远行冒险”还有很多,比如在竖式计算中,我们都知道从低位开始计算,这是“捷径”,那么“远行”就是:“竖式计算能不能从高位算起?”
再比如,我们知道图形的内角和,三角形180º,四边形360º,五边形540º,这是“捷径”。那么“冒险”就是“多边形的外角和是多少呢?”
在这一系列的活动中,我们并没有背诵任何口诀,而是通过提问,引发孩子的好奇心,从而推动孩子的探索和发现之旅。而主动探索之下,孩子们养成真正的主动思考习惯,才是思维“远行”的价值所在。
我们不能怪孩子没有独立思考的能力,因为很多时候,他们并没有思考的自由。远行需要花费更多的时间、精力和资源,但是与被浪费掉的生命而言,远行实在是性价比非常高的学习方法。数学本身足够美丽,让孩子把时间浪费在美好的事物上吧。
学好数学,需要进行创造
除了在好奇心的驱使下,让孩子进行更多的自主探索以外,数学的独立思考能力培养,还在于帮助孩子认识到数学的本质是一种有序的创造。
18世纪维科有一个著名的命题——“真理即创造之物,创造之物即真理。”他认为由于数学完全是人构筑起来的知识体系,所以(对于人而言)其真实可靠性最值得期待。
这个观点是有一点的争议,因为一般情况下,大家都会认为数学更接近于发现一种规律模式的思维状态,就好像无理数本来就在那里,数学家有幸找到了它。
但是从另一个方面,数学是一种语言,对客观世界进行着表征和述说,在这个视角,数学的创造属性展露无遗——创造一种高效而简洁的范式来表达世界,数位计数系统、方程、解析几何、微积分都是人类数学史上的伟大发明。
那么从数学启蒙教育来讲,认识发生论认为:“儿童的数学不是教会的,而是自己“发明”的”,皮亚杰的意思是说:孩子对数学的知识理解,不是简单的复制,而是认知结构主动建构、重组、改造的过程,这些知识的获得不是来自成人的直接教授,而是来自对数学经验的操作。
比如说,我们最常见的数字符号:1、2、3、4、5……9,在我们初次向孩子展示的时候,孩子往往都是从字符的表象来看待数字的,但是这并不是数学,我们希望的是孩子能够理解符号背后的想法。
所以我们可以用“远行”的思路,向孩子展现不同文化下的数字符号,文化本身只是一个方面,更重要的通过文化现象引导孩子去关注背后趋于一致的人类智慧——每一个符号代表了一种量的多少,以及数位和10以上的计数是怎么一回事。
也可以用“创造”的思路,让孩子自己发明数字符号,从而探索数字记录系统,比如:

孩子只有在能用自己发明方法去表达数学思想时,才能说他真正弄懂了,这个过程本质上是一种创造的过程,我们称为表征。除了简单的数字符号表征外,创造模式也能在帮助孩子理解各种数量关系,以及运算和应用题学习上,发挥很大的作用。
创造的过程,就是伟大的想象力和理性的交融。
新加坡数学教育强盛一时的秘密武器——数学建模,纠其本质,也同样运用了数学语言的自我创造策略。
在持续的探索中我们会不断地提出问题,这让我们深入地思考和学习。而探索思考多了,一定会有创造性的思维迸发,在尝试的过程中,之前探索的结论得到了不断的验证,所以创造和探索是分不开的。探索是归纳思维,创造是演绎思维,是独立思考发展的一对翅膀。
独立思考的“按钮”
学好数学需要在“冒险”和“创造”中构建孩子的独立思考能力,而开启这一过程的“按钮”正是孩子被激发出的好奇心。然而孩子们最珍贵的好奇心,恰恰也最容易受到破坏。
有时候,成年人对孩子没完没了的问题没有耐心,也没有意愿探究孩子的问题可能代表的实质含义,这实在是“寒了孩子的好奇心”呀。可以说,提出问题是孩子好奇心的最初也是非常重要的表现。
保罗·拉克哈特是布朗大学的数学教授,他曾自愿到纽约布鲁克林的圣安学校(St。 Ann’s School)教导K-12的数学课,希望能带给孩子们数学的美感,和充满想像力的一面。他在《一个数学家的叹息》一书中说到:“数学其实是原始的创造力和美学的感受力。”又说:“数学不是遵循指示,而是要创造出新的方向。”
他觉得,现在学校里的数学,最主要的问题出在没有“问题”,没有那些能够引发孩子思考的“问题”。这种情况在我看来,还有另一个变式,就是引发思考的问题太多,以至于孩子没有时间和空间思考。这两种表现其实是一种情况,用保罗的话来说:“这样学习数学是很可悲的,人类被成了训练有素的黑猩猩。”
诸如像: “这里有一个题型。这里是解答它的方法。这个会出现在考试里。今天的家庭作业是习题1-35 题。”这样无须动脑的反刍公式和演算,都不是真正的问题。一个真正符合人类天性的提问应该是例如:“质数是无止尽的吗?”“无限大是一个数字吗?”“在一个平面上用对称的方式铺磁砖的方法有多少种?”之类。
总之,一个好的问题应当:
1、开放而非封闭;
2、有趣,引发好奇,并能持续推动探索;
3、激发我们提出新的有趣问题。
那么,这样的问题,对孩子数学的独立思考有什么帮助呢?
《解决问题》一书的作者波利亚曾说:“对自己提出问题是解决问题的开始。”长久以来,我们一直把“解决问题”放在孩子数学或思维能力培养的核心地位,但实际上,在此之前,我们先要帮助孩子认识“什么是问题?”,然后是“发现问题、提出问题”,最后才是和“解决问题”。
鼓励孩子提出自己的问题,意味着点燃了独立思考的第一把火,也是他们思维“远行”或“创造”的首推力。我们不要嫌孩子提出的问题幼稚,我们都从婴孩成长起来,也都曾经问过同样的问题:“这是什么?”“这是怎么发生的?”以及“为什么?”并且提出这样问题的能力,在我们长大以后显得尤为珍贵。
同时,我们也不要害怕孩子绕行远路,绕行远路就是真实的思考——自己猜测与发现、尝试错误、经历创造性的挫折、产生灵感、拼凑出他们的解释和证明等等。而他们在冒险中艰难跋涉的每一步,都不会白费,都将成为他们人生必要之经验。
保护好孩子的好奇心,对于客观世界,对于抽象世界,都是同样重要的。好奇心让我们产生想法,正如高斯曾经说过的:“我们需要的是想法,不是符号。”(What we need are notions,not notations),
而用好奇心构建的独立思考力,是孩子学习数学的核心燃料!
在本文结束之前,问大家一个好玩的问题,希望对我们“冰封”已久的数学好奇心,能有小小的“化冻”作用:
我们都知道圆形面积公式是πr²,而我们在推导公式时,会用到下面这样的“切西瓜片”策略。那么我的问题是,有没有其他的方式来解释圆形面积的计算,请使用小学生能听懂的语言,想出来后可以和你的孩子一起分享。
(声明:本文仅代表作者观点,不代表新浪网立场。)
文章关键词:思维