例6.某校的教室A位于工地O的正西方向，且OA=200米，一部拖拉机从O点出发，以每秒5米的速度沿北偏西53°方向行驶，设拖拉机的噪声污染半径为130米，试问教室A是否在拖拉机的噪声污染范围内？若不在，请说明理由；若在，求出教室A受污染的时间有几秒？(已知：sin53°≈0.80, sin37°≈0.60, tan37°≈0.75)(福州)

　　说明：这种问题在近几年各地的中考题目中出现较多。
　　要求：1、要能准确画出辅助方位图；
　　2、完成从实际问题到几何模型的转化，转成解直角三角形的问题。

　　例7.如图的曲线表示一辆自行车离家的距离与时间的关系，骑车者九点离开家，十五点回家，根据这个曲线图，请你回答下列问题。

　　(1)到达离家最远的地方是什么时间？
　　(2)何时开始第一次休息？休息多长时间？
　　(3)第一次休息时，离家多远？
　　(4)11：00到12：00，他骑了多少千米？
　　(5)他在9：00~10：00和10：00~10：30的平均速度各是多少？
　　(6)他在何时至何时停止前进并休息用午餐？
　　(7)他在停止前进后返回，骑了多少千米？
　　(8)返回时的平均速度是多少？
　　(9)11：30和13：30时，分别离家多远。
　　(10)何时距离家22千米？

　　分析：这个曲线图，与课本上函数图象的不同点在于横轴表示的时间不是从0开始的，而是从9开始，横、纵轴上的数值代表着截然不同的实际含意。(t,S)

　　解：(1)12点，30千米
　　(2)10点半，半小时
　　(3)离家17千米
　　(4)11：00到12：00，他骑了13千米
　　(5)9：00~10：00的平均速度为10千米/时，
　　　10：00~10：30的平均速度是14千米/时
　　(6)12点到13点
　　(7)返回骑了30千米
　　(8)2小时，15km/h.

　　例8.有一批货，如果月初售出，可获利1000元，并可得本利和再去投资，到月末获利1.5%；如果月末售出这批货，可获利1200元，但要付50元保管费，请问这批货在月初还是月末售出好？

　　解：设这批货成本为a元，月初出售到月末可获利润
　　P1=1000+(a+1000)×1.5%=0.015a+1015
　　月末出售可获利润P2=1200-50=1150元
　　P1-P2=0.015(a-9000)
　　故为a>9000时，月初出售好；
　　当a=9000时，月初，月末出售相同；
　　当a<9000时，月末出售好。

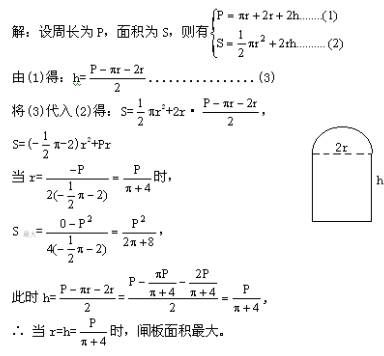
　　例9.某水库的闸板如图所示，它的形状是由一个半圆和一个矩形组合而成，为了周围封得好，周长应尽可能小，但为了使水的流量越大越好，希望面积尽可能地大，问当周长一定时半圆半径r和矩形高度h应怎样取才好呢？

　　分析：在周长一定的条件下，面积的大小即与r有关又与h有关，即S是r和h的函数，在含两个自变量的函数关系式中，通常由一个变量表示另一个，转化为含一个的再求最值。

　　说明：利用函数关系式求最值问题，在生活实际中有着广泛的应用，诸如周长最小，面积最大材料最省，效益最好等等，往往可以通过建立适当的函数关系式，通过求函数的最值来解决。