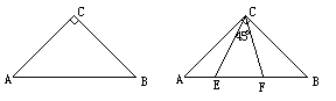
例3.如图，已知ΔABC是等腰直角三角形，∠C=90°

　　(1)操作并观察，如图，将三角板的45°角的顶点与点C重合，使这个角落在∠ACB的内部，两边分别与斜边AB交于E、F两点，然后将这个角绕着点C在∠ACB的内部旋转，观察在点E、F的位置发生变化时，AE、EF、FB中最长线段是否始终是EF？

　　写出观察结果。

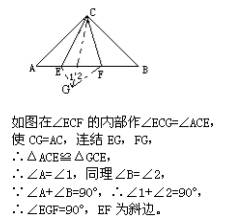
　　(2)探索：AE、EF、FB这三条线段能否组成以EF为斜边的直角三角形(即能否有EF2=AE2+BF2)？如果能，试加以证明。

　　分析：操作、观察不是重点，探索、猜测才是整个题目的重点，是难点，也就是说，从操作中获取信息是探索问题的过程中最重要的。
　　(1)中只须旋转∠ECF中用刻度尺量一量或观察，即可得到。
　　(2)要判断EF²=AE²+EF²，思路是把AE、EF、FB搬到一个三角形中，通常用平移、翻折、旋转等方法，此题目用翻折的方法，出现和线段AE、BF相等的线段，并且和EF在一个三角形中。

　　解：(1)观察结果是：当45°角的顶点与点C重合，并将这个角绕着点C在重合，并将这个角绕着点C在ÐACB内部旋转时，AE、EF、FB中最长的线段始终是EF。

　　(2)AE、EF、FB三条线段能构成以EF为斜边的直角三角形，证明如下：

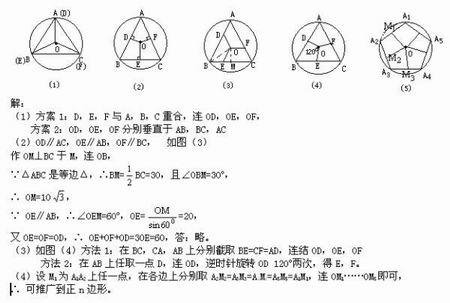
　　例4.(北京朝阳区，最后一题)如图，一个圆形街心花园，有三个出口A，B，C，每两个出口之间有一条60米长的道路，组成正三角形ABC，在中心点O处有一亭子，为使亭子与原有的道路相通，需再修三条小路OD，OE，OF，使另一出口D、E、F分别落在ΔABC分成三个全等的多边形，以备种植不同品种的花草。

　　(1)请你按以上要求设计两种不同的方案，将你的设计方案分别画在图1，图2中，并附简单说明。
　　(2)要使三条小路把ΔABC分成三个全等的等腰梯形，应怎样设计？请把方案画在图3中，并求此时三条小路的总长。
　　(3)请你探究出一种一般方法，使得出口D不论在什么位置，都能准确地找到另外两个出口E、F的位置，请写明这个方法。
　　(4)你在(3)中探究出的一般方法适用于正五边形吗？请结合图5予以说明，这种方法能推广到正n边形吗？

　　例5.某房地产公司要在一块地(图中矩形ABCD)上规划建造一个小区公园(矩形GHCK)，为了使文物保护区ΔAEF不被破坏，矩形公园的顶点G不能在文物保护区内，已知AB=200m, AD=160m, AE=60m, AF=40m。

　　(1)求矩形小区公园的顶点G恰是EF的中点时，公园的面积。
　　(2)当G在EF上什么位置时，公园面积最大？

　　分析：第一问比较容易，求出矩形GHCK的长和宽，注意利用ΔAEF的条件。
　　第二问是个探索性的问题，求面积的最大值，常用的办法是将面积表示成长(或者宽)的函数。

　　说明：对于探索某一个量最大、最小的问题，利用函数思想是首选的方法，可以设置适当的变量，所求的量用它来表示，从而用函数的最大最小来求。