2015广东公务员考试数量关系之趣味问题
相信各位考生都知道,在公考[微博]行测当中,数量关系主要考查报考者理解、把握事物间量化关系和解决数量关系问题的能力,主要涉及数据关系的分析、推理、判断、运算等,注重考查考生的逻辑思维能力,可能很多考生都会因为自身数学基础薄弱或者自己“智商不够”等各种原因惧怕这一部分,甚至全盘放弃,个人认为这是不可取的。数学运算部分有难题,可以选择性的放弃部分难题、偏题、怪题,但是数学运算当中有一大题型叫做趣味问题,只要考生可以合理有效地复习,这就是一大“低投入高产出”的题型,希望考生好好把握。
(一)趣味问题概述
所谓趣味问题,从字面意思就知道,这一大题型是非常有趣味性的,只要方法技巧适当掌握,学好了会觉得很有趣。
(二)题型分类
趣味问题主要包括牛吃草问题、年龄问题、余数问题、钟表问题、方阵问题、植树问题、统筹问题、剪绳问题等。这些题型的特征都非常的明显,以下就逐个做一个简单介绍:
牛吃草:本质就是一个有积累、有消耗,也有增长的问题,或者说是行程追及问题,或者工程问题,题干中常常会给出至少两组并列的数据,比如,有一片草地,12头牛吃4天,9头牛吃6天,那么多少头牛吃2天吃完?但是题干不一定就是给牛和草,换成人吸氧气,抽水机抽水等,本质都是一样的。
年龄问题:题干通常会给出多个人多个时间段的一个年龄关系,求其中某个人或多个人的年龄各自是多少,或者年龄和或年龄差是多少。
余数问题:余数问题有两种考查形式,第一是计算型的,涉及到被除数、除数、商和余数;第二种是公式型的,用公式计算即可,比如一个三位数,除4余3,除5余4,除3余2,这样的三位数有多少个?
钟表问题:钟表问题通常考察时针和分针的相对运动关系,实质为追及问题,如问某一时刻,时针和分针的夹角是多少度?;还会考察快慢钟的问题,实质为比例问题。
方阵问题:方阵问题实质为等差数列,通常考察方阵总数。
植树问题:植树问题实质为边端计数,需要记住不同植树方式的计数公式,比如600米的楼房之间,每隔50米植一颗树,一共能植几颗?
统筹问题:实质为资源最大利用,需要结合题干分析,稍有难度,是考试时可以适当放弃的题。
其他问题:如剪绳问题,过河爬井问题,空瓶换酒问题等等。
(三) 广东省历年命题规律
正所谓知己知彼百战百胜,考生们需要对广东省的趣味问题考情做一个了解,才能做到有的放矢,以下就是近7年广东省考趣味问题的一个基本情况:
| 08 | 09 | 10 | 11 | 12 | 12乡镇 | 13 | 13乡镇 | 14 | 14乡镇 | 总计 | 合计 | ||
| 趣味问题 | 牛吃草 | 1 | 1 |
14 |
|||||||||
| 年龄 | 1 | 1 | 1 | 3 | |||||||||
| 余数 | 1 | 1 | 2 | ||||||||||
| 钟表 | 1 | 1 | |||||||||||
| 方阵 | 1 | 1 | |||||||||||
| 植树 | 1 | 1 | 2 | ||||||||||
| 统筹 | 1 | 1 | 1 | 3 | |||||||||
| 其它 | 1 | 1 | |||||||||||
(四)典型例题分析
读完该图,相信大家也有了一个直观大体的把握,杂题题量并不大,几乎每年考1-2道,但是具体是哪些题型,每年均有所不同,所以希望大家在尽可能的情况下保证知识的广度,都要做一个了解,以下我就典型例题做出分析和建议。
【广东-2009】某矿井发生透水事故,且矿井内每分钟涌出的水量相等。救援人员调来抽水机抽水,如果用两台抽水机抽水,预计40分钟可抽完;如果用4台同样的抽水机,16分钟可抽完。为赢得救援时间,要求在10分钟内抽完矿井内的水。那么至少需要抽水机( )。
A.5台 B.6台
C.8台 D.10台
【解析】这是一道典型的牛吃草问题,设需要抽水机x台,涌出的水量相当于y台抽水机,则有:40(2-y)=16(4-y)=10(x-y),解得x=6,因此,本题答案为B。需要大家熟记牛吃草核心公式,Y=(n-x)t
或者使用列表法在10秒内解决是完全有可能的:
? ( ?-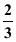 )× 10=160
)× 10=160
2 (2- ) × 40 =160 80
) × 40 =160 80
4 ( 4-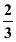 ) × 16=160 64
) × 16=160 64
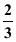 24 16
24 16
所以?=6台,B选项正确。
【广东-2010】办公室有甲、乙、丙、丁4位同志,甲比乙大5岁,丙比丁大2岁。丁三年前参加工作,当时22岁。他们四人现在的年龄之和为127岁。那么乙现在的年龄是( )。
A.25岁 B.27岁
C.35岁 D.40岁
【解析】典型的年龄问题,题干中给出了4个人的年龄关系,“丁三年前参加工作,当时22岁”,则丁今年25岁;”丙比丁大2岁”,则丙今年27岁,根据题意有:甲=乙+5,甲+乙+丙+丁=乙+5+乙+27+25=127,解得乙=35,则乙现在的年龄是35岁,因此,本题答案为C。只要理清不同人之间的关系,使用方程便能很快解出本题。
【广东-2011】三位运动员跨台阶,台阶总数在100-150级之间,第一位运动员每次跨3级台阶,最后一步还剩2级台阶。第二位运动员每次跨4级台阶,最后一步还剩3级台阶。第三位运动员每次跨5级台阶,最后一步还剩4级台阶。则这些台阶总共有( )级。
A.119 B.121
C.129 D.131
【解析】本题属于余数问题,可以选择代入排除,A选项正确;或者将台阶总数+1分别能被3、4、5整除,A正确;或者使用差同减差的通式,3…2,4…3,5…4,取3、4、5的最小公倍数60,再减共同的差1,故公式为60n-1,范围在100-150之间,所以n取2,答案为60×2-1=119,A正确。希望各位考生能熟练运用差同减差、和同加和、余同加余的通式。
【广东-2012】小张的手表和闹钟走时都不准,手表比标准时间每6小时快2分钟,闹钟比标准时间每6小时慢5分钟。一天,小张发现手表指示9点27分时,闹钟刚好指示9点41分,那么至少要经过( )小时,手表和闹钟才能指示同一时刻。
A. 6 B. 9
C. 12 D. 13
【解析】这是一道钟表问题中的快慢钟问题,就是考查的比例关系。根据题意,手表每6小时比闹钟快2+5=7分钟,而现在手表比闹钟慢14分钟,因此需要2个6小时赶上,即12小时。因此,答案选择C选项。
【广东-2012】有绿、白两种颜色且尺寸相同的正方形瓷砖共400块。将这些瓷砖铺在一块正方形的地面上:最外面的一周用绿色瓷砖铺,从外往里数的第二周用白色的瓷砖铺,第三周用绿色瓷砖,第四周用白色瓷砖……这样依次交替铺下去,恰好将所有瓷砖用完。这块正方形地面上的绿色瓷砖共有( )块。
A.180 B.196
C.210 D.220
【解析】方阵问题,共有瓷砖400块,则最外面一边为20块,由外到内每边瓷砖数依次为20,18,16,14,12…。而其中绿色瓷砖的边长为20,16,12,8,4。因此总共用绿色瓷砖数为(20-1)×4+(16-1)×4+(12-1)×4+(8-1)×4+(4-1)×4=220。因此,答案选择D选项。或者这样理解,因为一共400块,绿色在外围,一层绿色和一层白色循环摆放,所以绿色瓷砖总数必定大于白色瓷砖数,排除AB,而且根据方阵每边人数=4n-4可知,每边瓷砖为4的倍数,所有绿色瓷砖加起来也是4的倍数,D选项正确。考生需牢记方阵最外围人数=4n-4,方阵总人数= 。
。
【广东-2013】小陈家住在5楼,他每天上下楼各一次,共需要走120级楼梯。后来,小陈家搬到同一栋楼的8楼,如果每层楼的楼梯级数相同,则他搬家后每天上下楼各一次共需要走楼梯( )级。
A.168 B.192
C.210 D.240
【解析】边端计数问题,由题意可知,小陈上5楼需要爬四层,每上下一层需要走120÷4=30级楼梯,搬到8楼后,需要上下7层,所以共需要走楼梯30×7=210级楼梯,C选项正确。本题一定要注意,上5楼并不需要爬5层,只需要爬4层,上到n层楼梯只需要爬n-1层。
【广东-2011】一个产品生产线分为abc三段,每个人每小时分别完成10、5、6件,现在总人数为71人,要使得完成的件数最大,71人的安排分别是( )。 A.14:28:29 B.15:31:25
C.16:32:23 D.17:33:21
【解析】统筹问题,每个人每小时分别完成10、5、6件,赋总数为30件时,第一第二第三段的效率比3:5:6,最接近这个比值的答案为B选项。因此,本题答案为B。统筹问题的原则就是花最少的资源尽可能多做事情。
【广东-2013】某礼堂的观众座椅共96张,分东、南、西三个区域摆放。现从东区搬出与南区同样多的座椅放到南区,再从南区搬出与西区同样多的座椅放到西区,最后从西区搬出与东区剩下的座椅数量相同的座椅放到东区,这时三个区域的座椅数量相同。则最初南区的座椅有( )张。
A.24 B.28
C.32 D.36
【解析】本题中间过程复杂,可以考虑倒过来推算,由最后一列开始填数字,根据题干条件推算其它的数据,最后得出结论。由题意可知,第三次搬运后三区的座椅数量均为96÷3=32张。所以按照第3次,第2次,第1次的顺序倒搬,填出数字,发现南区最初由28张,B选项正确。
东 南 西
初始状态 44 28 24
第1次搬 16 56 24
第2次搬 16 32 48
第3次搬 32 32 32
由于时间和篇幅的限制,趣味问题在此并没有完全展开,希望广大考生安排好复习时间,合理有效地对这一部分进行学习和强化,将这一难度并不是很大的模块顺利的拿下,最终获得笔试的理想成绩。
特别说明:由于各方面情况的不断调整与变化,新浪网所提供的所有考试信息仅供参考,敬请考生以权威部门公布的正式信息为准。
文章关键词: 2015广东公务员考试公务员考试
- 2015广东公务员考试数量关系之容斥问题2015-02-05 17:51
- 2015广东公务员考试数量关系之数字推理2015-02-05 17:45
- 2015广东公务员考试言语模块之细节理解分析2015-02-05 17:39
- 2015广东公务员考试言语模块之主旨概括分析2015-02-05 17:36
- 2015广东公务员考试主旨概括考点命题分析2015-02-05 17:11
- 2015年广东公务员考试言语模块之意图题2015-02-05 16:54

