2.函数概念与基本初等函数Ⅰ(指数函数、对数函数、幂函数)

　　(1)函数

　　①了解构成函数的要素，会求一些简单函数的定义域和值域；了解映射的概念。

　　②在实际情境中，会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数。

　　【试题举例】

　　已知函数f(x)，g(x)分别由下表给出

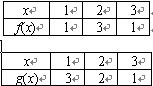
　　则f[g(1)]的值是　；满足f[g(x)]>g[f(x)]的x的值是　.

　　【答案】1；2

　　【解析】由表格中的函数关系可得f[g(1)]＝f(3)＝1.

　　函数f[g(x)]与g[f(x)]对应的函数关系如下表所示：

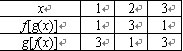
　　由上表函数关系式可得，当且仅当x＝2，f[g(x)]＞g[f(x)]成立，

　　∴满足f[g(x)]＞g[f(x)]的x的值为2.

　　③了解简单的分段函数，并能简单应用。

　　【试题举例】(2008·北京)

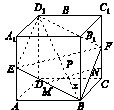
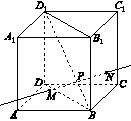
　　如图，动点P在正方体ABCD－A1B1C1D1的对角线BD1上，过点P作垂直于平面BB1D1D的直线，与正方体表面相交于M，N.设BP＝x，MN＝y，则函数y＝f(x)的图象大致是(　)

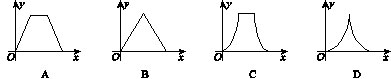
　　【答案】B

　　【解析】

　　过点BD1作垂直于B1BDD1的垂面，即D1EBF，

　　∵P在MN上，故MN⊂面D1EBF，当M在BE上时，tan∠D1BE＝MP/BP＝1/2y/x，∵∠D1BE为定角，故y与x成线性关系，同时关于EF对称，正确答案B.此题属于难题，学生不易分析和求解。

　　④理解函数的单调性、最大值、最小值及其几何意义；结合具体函数，了解函数奇偶性的含义。

　　【试题举例】

　　已知定义域为R的函数f(x)在(8，＋∞)上为减函数，且函数y＝f(x＋8)为偶函数，则(　)

　　A.f(6)>f(7) B.f(6)>f(9) 

　　C.f(7)>f(9) D.f(7)>f(10)

　　【答案】D

　　【解析】∵y＝f(x＋8)为偶函数， ∴f(－x＋8)＝f(x＋8)， ∴x＝8是函数f(x)的一条对称轴， 又∵f(x)在(8，＋∞)上为减函数，∴f(x)在(－∞，8)上为增函数，∴f(6)＝f(10)＜f(7)＝f(9)，故应选D.

　　⑤会运用函数图象理解和研究函数的性质。

　　【试题举例】

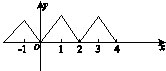
　　在R上定义的函数f(x)是偶函数，且f(x)＝f(2－x).若f(x)在区间[1,2]上是减函数，则f(x)(　)

　　A.在区间[－2，－1]上是增函数，在区间[3,4]上是增函数

　　B.在区间[－2，－1]上是增函数，在区间[3,4]上是减函数

　　C.在区间[－2，－1]上是减函数，在区间[3,4]上是增函数

　　D.在区间[－2，－1]上是减函数，在区间[3,4]上是减函数

　　【答案】B

　　【解析】考查函数性质，由f(x)＝f(2－x)得f(x)的对称轴为x＝1.又由偶函数得f(x)图象关于y轴也对称。在[1,2]上为减函数，画出示意图可得。

　　【导读】函数是高考数学中极为重要的内容，函数的观点和方法既贯穿了高中代数的全过程，又是学习高等数学的基础。纵观近几年来的高考试题，函数在选择、填空、解答三种题型中每年都有试题，约占全卷的30%左右，函数的性质及图象变换多以选择题形式出现，并且低难度和高难度的试题都有可能出现。函数的解答题，综合性较强，难度较大，要进行周密地分析、准确地计算来解决。关于这部分的应用题，不仅有解答题，还可能有选择题或填空题。高考正在逐步增加应用题的考查力度，并且应用问题多在知识网络交汇处命题。因此，在复习过程中应注意加强对分析问题、解决综合问题能力方面的训练。

　　近几年的高考真题对函数的考查常着重如下方面：

　　①对函数的概念、基本性质及图象的考查主要以小题的形式出现，在学习、复习函数时，要坚持“定义(概念)→解析式→图象→性质”这条主线。

　　②函数与不等式、数列、向量、解析几何等知识的综合问题会以解答题形式出现，属于理解、灵活运用层次，难度较大。解答上述问题时要注意数学思想方法的应用，函数这一章重要的数学思想方法有方程与函数的思想、分类讨论的思想、等价转化的思想、数形结合的思想，数学方法有配方法、换元法、待定系数法、比较法等。

　　③通过函数应用题考查建立函数模型及解读信息的能力，体现了新课标重视应用能力的考查，注意培养学生阅读、理解能力，提炼数学问题的能力，以及用数学语言表达的能力，要求学生仔细阅读，抓住信息，透彻理解，准确解题。

　　④新课标新增内容中与函数有关的内容——特别是函数的零点将是高考的热点，以函数为载体考查方程根的个数的判断，以及求参数的取值范围将是重点考查的问题。

　　(2)指数函数

　　①了解指数函数模型的实际背景。

　　②理解有理指数幂的含义，了解实数指数幂的意义，掌握幂的运算。

　　③理解指数函数的概念，理解指数函数的单调性，掌握指数函数图象通过的特殊点。

　　【试题举例】

　　若函数f(x) ＝√2x2＋2ax－a－1的定义域为R，则a的取值范围为　.

　　【答案】[－1,0]

　　【解析】由题意可得2x2＋2ax－a－1≥0恒成立， 即2x2＋2ax－a≥1，∴x2＋2ax－a≥0恒成立，　∴Δ＝4a2＋4a≤0，解之得a∈[－1,0].

　　④知道指数函数是一类重要的函数模型。

　　(3)对数函数

　　①理解对数的概念及其运算性质，知道用换底公式能将一般对数转化成自然对数或常用对数；了解对数在简化运算中的作用。

　　【试题举例】(2008·广东)

　　设a∈R，若函数y＝eax＋3x，x∈R有大于零的极值点，则(　)

　　A.a<－1/3 B.a>－1/3 C.a<－3 D.a>－3

　　【答案】C

　　【解析】解决本题的关键是要理解“函数有大于零的极值点”这一条件。由题意，根据导数公式，得y′＝3＋aeax，若函数y＝eax＋3x，x∈R有大于零的极值点，说明方程y′＝3＋aeax＝0有正根，即eax＝－3/a有正根，显然需a<0.此时，x＝1/aln(－3/a)，由x>0立即可解得参数a<－3.故答案为C.

　　②理解对数函数的概念，理解对数函数的单调性，掌握对数函数图象通过的特殊点。

　　③知道对数函数是一类重要的函数模型。

　　【试题举例】

　　设f(x)＝lg（2/1－x＋a）是奇函数，则使f(x)＜0的x的取值范围是(　)

　　A.(－1,0) B.(0,1) 

　　C.(－∞，0) D.(－∞，0)∪(1，＋∞)

　　【答案】A

　　【解析】由函数f(x)＝lg（2/1－x＋a）为奇函数，可得f(0)＝lg(2＋a)＝0，

　　解之得2＋a＝1，即a＝－1，∴f(x)＝lg（2/1－x＋a）＝lg1+x/1-x，由f(x)＜0可得lg1+x/1-x＜0，即0＜1+x/1-x＜1，解之得－1＜x＜0， 由此可得的x取值范围为(－1,0)， 故应选A.

　　点评：本题通过对数复合函数与函数的奇偶性及函数不等式的求解等知识点的交汇，考查了考生对函数的性质及不等式的解法的掌握，以及灵活选择解题策略，决定解题方向的解题机智。

　　④了解指数函数y＝ax与对数函数y＝logax互为反函数(a>0，且a≠1).

　　【试题举例】

　　函数y＝f(x)的图象与函数y＝log3x(x＞0)的图象关于直线y＝x对称，则f(x)＝　.

　　【答案】3x(x∈R)

　　【解析】本小题主要考查原函数与反函数图象间的关系及反函数的求解问题。本题转化为求y＝log3x(x＞0)的反函数。即f(x)＝3x.但一定要注明f(x)的定义域x∈R.

　　(4)幂函数

　　①了解幂函数的概念。

　　②结合函数y＝x，y＝x2，y＝x3，y＝1/x，y＝x1/2的图象，了解它们的变化情况。

　　【试题举例】

　　设a∈{－1，1，12，3}，则使函数y＝xa的定义域为R且为奇函数的所有a值为(　)

　　A.1,3 B.－1,1 C.－1,3 D.－1,1,3

　　【答案】A

　　【解析】本题可作出上述几种常见幂函数图象，观察图象即可作出判断。

　　(5)函数与方程

　　①结合二次函数的图象，了解函数的零点与方程根的联系，判断一元二次方程根的存在性及根的个数。

　　②根据具体函数的图象，能够用二分法求相应方程的近似解。

　　【试题举例】(2008·山东)

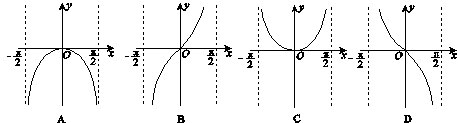
　　函数y＝lncosx(－π/2<x<π/2)的图象是(　)

　　【答案】A

　　【解析】本题考查函数中的识图问题，给出解析式后，应该利用函数性质作出判断。常用到函数的定义域、值域、单调性、奇偶性、周期性、特殊值等性质。显然函数是偶函数，故排除B，D，又因为0<cosx<1，∴lncosx<0，故选A.

　　(6)函数模型及其应用

　　①了解指数函数、对数函数以及幂函数的增长特征，知道直线上升、指数增长、对数增长等不同函数类型增长的含义。

　　②了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用。

　　【试题举例】

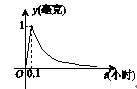
　　为了预防流感，某学校对教室用药熏消毒法进行消毒。已知药物释放过程中，室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比；药物释放完毕后，y与t的函数关系式为y＝(1/16)t－a(a为常数)，如图所示。根据图中提供的信息，回答下列问题：

　　(Ⅰ)从药物释放开始，每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为　；

　　(Ⅱ)据测定，当空气中每立方米的含药量降低到0.25毫克以下时，学生方可进教室，那么从药物释放开始，至少需要经过　小时后，学生才能回到教室。

　　【答案】y＝{10t(0≤t≤1/10)，1/16t－1/10(t＞1/10).；0.6

　　更多高考信息请访问：新浪高考频道 高考论坛 高考博客圈 高考贴吧

　　特别说明：由于各方面情况的不断调整与变化，新浪网所提供的所有考试信息仅供参考，敬请考生以权威部门公布的正式信息为准。