3.立体几何初步

　　(1)空间几何体

　　①认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构。

　　【试题举例】

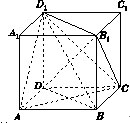
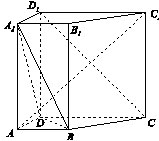
　　在正方体上任意选择4个顶点，它们可能是如下各种几何形体的4个顶点，这些几何形体是　(写出所有正确结论的编号).

　　①矩形；

　　②不是矩形的平行四边形；

　　③有三个面为等腰直角三角形，有一个面为等边三角形的四面体；

　　④每个面都是等边三角形的四面体；

　　⑤每个面都是直角三角形的四面体。

　　【答案】①③④⑤

　　【解析】本题主要考查立体几何中的概念，几何图形的性质，属于综合知识能力的考查。如图四边形BB1D1D为矩形；四面体B1ACD1满足选项④；四面体A1AB1D1满足选项③；四面体ABD1D满足选项⑤.

　　②能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图，能识别上述三视图所表示的立体模型，会用斜二测法画出它们的直观图。

　　【试题举例】

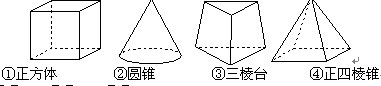
　　下列几何体各自的三视图中，有且仅有两个视图相同的是(　)

　　A.①② B.①③ C.①④ D.②④

　　【答案】D

　　【解析】根据三视图的概念易知②④有且仅有两个视图相同。

　　③会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图，了解空间图形的不同表示形式。

　　④会画某些建筑物的视图与直观图(在不影响图形特征的基础上，尺寸、线条等不作严格要求).

　　【试题举例】

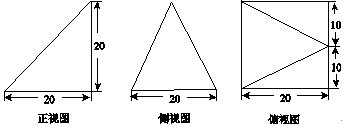
　　已知某个几何体的三视图如右，根据图中标出的尺寸(单位：cm)，可得这个几何体的体积是(　)

　　【答案】B

　　【解析】本题考查三视图的知识及几何体体积公式等知识。根据三视图的知识及特点，可画出几何体形状，为如图所示的四棱锥。且底面为边长是20的正方形，高VH＝20，所以这个几何体的体积V＝1/3×20×20×20＝8000/3cm3.

　　⑤了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式).

　　【试题举例】

　　已知三棱锥S－ABC的各顶点都在一个半径为r的球面上，球心O在AB上，SO⊥底面ABC，AC＝√2r.则球的体积与三棱锥体积之比是(　)

　　A.π B.2π C.3π D.4π

　　【答案】D

　　【解析】本题考查球及球的组合体以及球的体积和棱锥的体积公式等知识。由于三棱锥各顶点都在球面上，且球心O在AB上，SO⊥底面ABC，所以AB为球的一条直径，且AO＝BO＝SO＝r，AC＝√2r.所以三棱锥S－ABC为底面是等腰直角三角形，高SO＝r的棱锥，其体积是S＝1/3·S△ABC·SO＝1/3×1/2×√2r×√2r×r＝r*r*r/3，球的体积S＝4/3πr3，所以球的体积与三棱锥的体积之比为4π.

　　(2)点、直线、平面之间的位置关系

　　①理解空间直线、平面位置关系的定义，并了解如下可以作为推理依据的公理和定理。

　　公理1：如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在此平面内。

　　公理2：过不在同一条直线上的三点，有且只有一个平面。

　　公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。

　　公理4：平行于同一条直线的两条直线互相平行。

　　定理：空间中如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补。

　　【试题举例】

　　在平面上，两条直线的位置关系有相交、平行、重合三种. 已知α、β是两个相交平面，空间两条直线l1、l2在α上的射影是直线s1、s2，l1、l2在β上的射影是直线t1、t2.用s1与s2，t1与t2的位置关系，写出一个总能确定l1与l2是异面直线的充分条件：　.

　　【答案】s1∥s2，并且t1与t2相交(t1∥t2，并且s1与s2相交)

　　【解析】 若两条直线在一个平面内的射影为一对平行直线，则这两直线平行或异面， 由此结论知，只需要该直线在另一平面内的射影满足是两条相交直线即可. 故可以填：s1∥s2 ，并且t1与t2相交(t1∥t2，并且s1与s2相交).

　　②以立体几何的上述定义、公理和定理为出发点，认识和理解空间中线面平行、垂直的有关性质与判定定理。

　　理解以下判定定理。

　　如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行。

　　如果一个平面内的两条相交直线与另一个平面都平行，那么这两个平面平行。

　　如果一条直线与一个平面内的两条相交直线都垂直，那么该直线与此平面垂直。

　　如果一个平面经过另一个平面的垂线，那么这两个平面互相垂直。

　　理解以下性质定理，并能够证明。

　　如果一条直线与一个平面平行，那么经过该直线的任一个平面与此平面的交线和该直线平行。

　　【导读】1.准确理解、熟练掌握性质定理并能进行三种语言(文字语言、符号语言和图形语言)的转化是关键。

　　2.一般在已知中知道线面平行时就要考虑运用线面平行的性质定理；在求证线线平行时也要想到可能要运用线面平行的性质定理。

　　3.在运用线面平行的性质定理时，要特别注意“一条直线平行于一个平面，就平行于这个平面的一切直线”的错误结论。

　　4.直线与平面平行的性质定理实质就是线线平行与线面平行的转化，转化的思想方法贯穿于整个立体几何中。

　　如果两个平行平面同时和第三个平面相交，那么它们的交线相互平行。

　　垂直于同一个平面的两条直线平行。

　　如果两个平面垂直，那么一个平面内垂直于它们交线的直线与另一个平面垂直。

　　③能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题。

　　【试题举例】

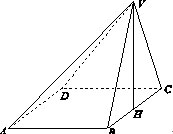
　　如图，在直四棱柱ABCD—A1B1C1D1中，已知DC＝DD1＝2AD＝2AB，AD⊥DC，AB∥DC.

　　(Ⅰ)求证：D1C⊥AC1；

　　(Ⅱ)设E是DC上一点，试确定E的位置，使D1E∥平面A1BD，并说明理由。

　　【解析】(Ⅰ)证明略。

　　(Ⅱ)当E是CD中点时，

　　可使D1E∥平面A1BD.

　　【导读】新课标教材中对立体几何的内容编排作了大胆的改进，即将旧教材中以位置关系为主线，从局部到整体的内容展开形式变为以图形特征为主线，从整体到局部(从柱，锥，台球到点、线、面)，更容易帮助学生完善思维结构，发展空间想象能力，“立体几何初步”是以三个载体(三视图、直观图、点线面的位置关系)来帮助学生认识空间图形及其位置关系，建立空间想象能力。并在几何直观的基础上，初步形成对空间图形的逻辑推理能力。复习中注意如下方面：

　　①明确柱、锥、台、球的几何特征，并能进行表面积、体积、球的球面距离的运算是高考考查的重点之一。高考以此为载体考查空间想象能力及运算能力。

　　②新课程“立体几何”部分新增了一些内容：平行投影、中心投影、三视图，特别是三视图将是高考的重点和热点，要求学生能够画出空间几何体的三视图和直观图，能够从空间几何体的直观图画出它的三视图，从三视图画出它的直观图等。使得学生能够通过“实物模型—三视图—直观图”这样一个相互转化的过程认识空间几何体，培养和发展学生的几何直观能力和空间想象能力，更全面地把握空间几何体。

　　③对空间位置关系特别是空间中的平行与垂直关系的考查将是高考必考内容，要将平行与垂直的判定定理及性质定理灵活应用，着重考查学生的空间想象能力和逻辑推理论证的能力。

　　更多高考信息请访问：新浪高考频道 高考论坛 高考博客圈 高考贴吧

　　特别说明：由于各方面情况的不断调整与变化，新浪网所提供的所有考试信息仅供参考，敬请考生以权威部门公布的正式信息为准。