4.平面解析几何初步

　　(1)直线与方程

　　①在平面直角坐标系中，结合具体图形，确定直线位置的几何要素。

　　②理解直线的倾斜角和斜率的概念，掌握过两点的直线斜率的计算公式。

　　③能根据两条直线的斜率判定这两条直线平行或垂直。

　　④掌握确定直线位置的几何要素，掌握直线方程的几种形式(点斜式、两点式及一般式)，了解斜截式与一次函数的关系。

　　⑤能用解方程组的方法求两条相交直线的交点坐标。

　　⑥掌握两点间的距离公式、点到直线的距离公式，会求两条平行直线间的距离。

　　【试题举例】

　　已知直线l过点P(2,1)，且与x轴、y轴的正半轴分别交于A、B两点，O为坐标原点，则△OAB面积的最小值为　.

　　【答案】4

　　【解析】本题考查直线方程。均值不等式等。

　　设A(a,0)，B(0，b)，由题意知a＞0，b＞0.

　　直线AB：x/a＋y/b＝1.P(2,1)在直线上。

　　∴2/a＋1/b＝1

　　∴1＝2/a＋1/b≥2√2/ab

　　∴ab≥8

　　∴S△AOB＝1/2ab≥4

　　等号成立条件：b＝2，a＝4.

　　(2)圆与方程

　　①掌握确定圆的几何要素，掌握圆的标准方程与一般方程。

　　【试题举例】

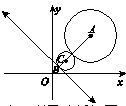
　　与直线x＋y－2＝0和曲线x2＋y2－12x－12y＋54＝0都相切的半径最小的圆的标准方程是　.

　　【答案】(x－2)2＋(y－2)2＝2

　　【解析】本题考查学生数形结合思想，以及分析问题、解决问题的能力。如图，显然当两圆圆心的连线与已知直线垂直时，所求圆的半径最小。把圆方程化为标准方程得：(x－6)2＋(y－6)2＝18，所以圆心A(6,6)，半径R＝3√2.由点A到直线x＋y－2＝0的距离d＝|6＋6－2|/√2＝5√2，所以动圆的半径r＝√2，再设动圆圆心C(x0，y0)，由AC⊥l，

　　所以y0－6/x0－6＝1⇒x0＝y0..................(1)

　　又因为点C到直线l的距离为r，

　　所以√2＝|x0＋y0－2|/√ 2............................(2)，由(1)、(2)得x0＝2，y0＝2.所以所求圆的标准方程为：(x－2)2＋(y－2)2＝2.

　　②能根据给定直线、圆的方程判断直线与圆的位置关系；能根据给定两个圆的方程判断两圆的位置关系。

　　【试题举例】

　　在平面直角坐标系xOy中，已知圆x2＋y2－12x＋32＝0的圆心为Q，过点P(0,2)且斜率为k的直线与圆Q相交于不同的两点A、B.

　　(Ⅰ)求k的取值范围；

　　(Ⅱ)是否存在常数k，使得向量OA＋OB与PQ共线？如果存在，求k值；如果不存在，请说明理由。

　　【解析】(Ⅰ)圆的方程可写成(x－6)2＋y2＝4，所以圆心为Q(6,0).过P(0，2)且斜率为k的直线方程为y＝kx＋2，代入圆的方程得x2＋(kx＋2)2－12x＋32＝0，整理得　(1＋k2)x2＋4(k－3)x＋36＝0.　①

　　直线与圆交于两个不同的点A、B等价于Δ＝[4(k－3)]2－4×36(1＋k2)＝42(－8k2－6k)＞0，解得－3/4<k<0，即k的取值范围为(－3/4，0).

　　(Ⅱ)设A(x1，y1)，B(x2，y2)，则OA＋OB＝(x1＋x2，y1＋y2)，由方程①，

　　x1＋x2＝－4(k－3)/1＋k2.　②

　　又y1＋y2＝k(x1＋x2)＋4.　③

　　而P(0,2)，Q(6,0)，PQ＝(6，－2).

　　所以OA＋OB与PQ共线等价于－2(x1＋x2)＝6(y1＋y2)，

　　将②③代入上式，解得k＝－3/4.

　　由(Ⅰ)知k∈(－3/4，0)，故没有符合题意的常数k.

　　③能用直线和圆的方程解决一些简单的问题。

　　④初步了解用代数方法处理几何问题的思想。

　　【试题举例】

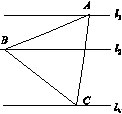
　　如图，l1、l2、l3是同一平面内的三条平行直线，l1与l2间的距离是1，l2与l3间的距离是2，正三角形ABC的三顶点分别在l1、l2、l3上，则△ABC的边长是(　)

　　A.2√3 B.4√6/3 C.3√17/4 D.2√

　　【答案】D

　　【解析】本题着重以平面几何为载体考查解析几何中两点间距离问题。建立以B为坐标原点，l2为x轴的平面直角坐标系。则：l1：y＝1，l3：y＝－2，设A(x1,1)，C(x2，－2)，则由题意知|OA|＝|OC|， ∴x＋1＝x＋4 …①

　　cos＜OA，OC＞＝，∴cos60°＝， ∴x＋1＝2x1x2－4……②

　　由①②得x2＝－2x1(舍) 或4x1＝5x2………③，将③代入①得x＋1＝x＋4，∴x＝，||＝＝＝.故选D.

　　(3)空间直角坐标系

　　①了解空间直角坐标系，会用空间直角坐标表示点的位置。

　　②会推导空间两点间的距离公式。

　　更多高考信息请访问：新浪高考频道 高考论坛 高考博客圈 高考贴吧

　　特别说明：由于各方面情况的不断调整与变化，新浪网所提供的所有考试信息仅供参考，敬请考生以权威部门公布的正式信息为准。