2015国考行测数学运算:植树问题
植树问题虽然在国家公务员[微博]考试行测科目中并不常见,但做好此类题不仅能锻炼数学思维,对解答其他题型也有一定帮助。中公教育[微博]专家在此进行详细解读。
一、植树问题的类型和应对公式
例如:在一周长为100米的湖边种树,如果每隔5米种一棵,共要种多少棵树?这样在一条“路”上等距离植树就是植树问题。在植树问题中,“路”被分为等距离的几段,段数=总路长÷间距、总路长=间距×段数。
根据植树路线的不同以及路的两端是否植树,段数与植树的棵数的关系式也不同,下面就从不封闭路线的植树和封闭路线植树来一一说明。
(1)不封闭植树:指在不封闭的直线或曲线上植树,根据端点是否植树,还可细分为以下三种情况:
①两端都植树:两个端点都植树,树有6棵,段数为5段,即有植树的棵数=段数+1,结合段数=总路长÷间距,则:棵数=总路长÷间距+1,总路长=(棵数-1)×间距。
②两端都不植树:两个端点都不植树,可知植树的棵数=段数-1,结合段数=总路长÷间距,则:棵数=总路长÷间距-1,总路长=(棵树+1)×间距。
③只有一端植树:只有一个端点植树,可知植树的棵数=段数,结合段数=总路长÷间距,则:棵数=总路长÷间距,总路长=棵数×间距。
(2)封闭植树:指在圆、正方形、长方形、闭合曲线等上面植树,因为头尾两端重合在一起,所以种树的棵数等于分成的段数。所以棵数=总路长÷间距,总路长=棵数×间距。
为方便记忆,将植树问题的公式归纳如下表:

二、两边植树问题
除了在路的一边植树外,还有路的两边都植树的情况,这时就要先判断出植树类型,计算出一边植树的情况,再根据一边求两边情况。
【例题1】如果每500米远架一根电线杆,则30公里需要架设多少根电线杆?
A.31 B.30 C.61 D.60
中公解析:此题答案为C。共需要架设30×1000÷500+1=61根电线杆。
三、不同间隔植树问题
在一些植树问题中,往往存在两种或多种植树方式。这种情况下,就会出现重复植树问题,常需要结合最小公倍数找出重合点。
【例题2】某工地从一条直道的一端到另一端每隔3米打一个木桩,一共打了49个木桩。现在要改成4米打一个木桩,那么可以不拔出的木桩共有多少个?
A.8 B.9 C.11 D.13
中公解析:此题答案为D。每隔3米打一木桩对应每隔3米植树,两端都打对应两端都植树,因此直道的总长=段数×间距=(棵数-1)×间距=(49-1)×3=144米。
依题意,不拔出来的木桩距离起点的距离必须能被3和4整除,3和4的最小公倍数是12,即从起点开始每隔12米有一个木桩可以不拔出,144÷12=12,故有12+1=13根木桩不用拔出。
四、植树问题变形
在数学运算中还有一些变形题,如锯木头、走楼梯等实际问题,这些变形只是形式上的改变,其本质仍然是植树问题。中公教育专家发现,在最近几年的行测考试中,植树问题往往以这种变形题出现。
解决植树问题的变形题,要注意端点是否“植树”,分清“棵数”与“段数”之间是+1还是-1。
常见的变形题:锯木头、爬楼梯、重合、队列问题均可视为两端都不植树问题,其中的知识要点如下:
锯木头:要锯成n段,则需锯(n-1)次;
爬楼梯:从1层到n层,需爬(n-1)段楼梯;若每爬完一段,休息一次,则需休息(n-2)次;
重合问题:n段接在一起,重合的有n-1段;
队列问题:有n个人(或n辆车),中间有n-1个空。
【例题3】把一根钢管锯成小段,一共花了28分钟。已知每锯开一段需要4分钟,这根钢管被锯成了多少段?
A.3 B.4 C.6 D.8
中公解析:此题答案为D。要求钢管被锯的段数,必须首先求出钢管被锯开几处。
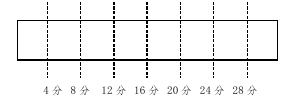
从上图我们可以看出钢管有28÷4=7处被锯开,因而锯开的段数有7+1=8段。题中被锯开的地方即植树位置,因此问题相当于“两端都不植树”问题,棵数=段数-1。
中公教育专家建议考生们将以上内容进行认真研究,为行测高分奠定牢固基础。
本文由中公教育供稿
- 公务员行测必考必会:数学运算2014-08-21 15:31
- 2015国考行测数学运算:鸡兔同笼练习题2014-08-20 10:28
- 2015国考行测数学运算:鸡兔同笼问题讲解2014-08-20 10:25
- 国考行测数学运算:容斥和抽屉原理练习2014-08-13 11:22
- 2015国考行测数学运算:容斥和抽屉原理2014-08-13 11:16
- 2015国考行测:数学运算之类比转化思维2014-08-12 10:01
















新浪警示:任何收费预测彩票会员等广告皆为诈骗,请勿上当!点击进入详情