不支持Flash
|
知识大盘点:集合与常用逻辑用语
第三章 知识大盘点
高考数学知识网络图:
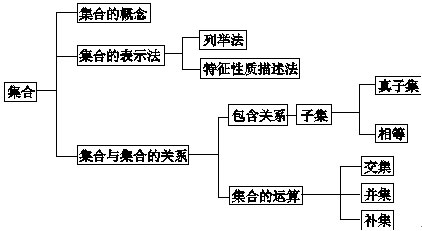
1.集合与常用逻辑用语
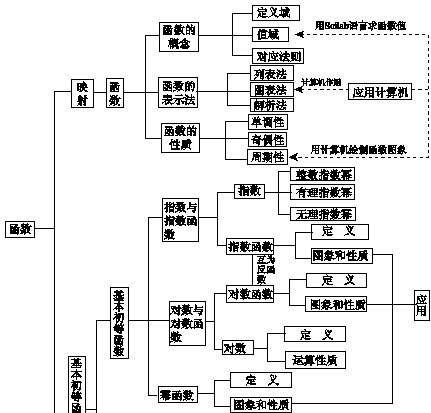
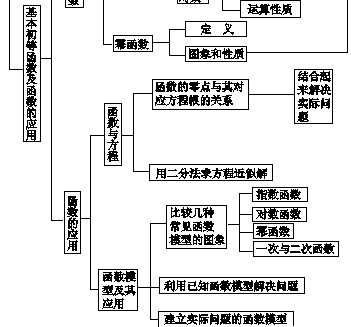
2.函数及基本初等函数(Ⅰ)
(1)
(2)指数函数图象和性质
|
a |
a>1 |
0<a<1 |
|
y=ax |
||
|
定义域 |
R |
R |
|
值域 |
x≥0时,y≥1 |
x≥0时,0<y≤1 |
|
定点 |
过点(0,1) |
过点(0,1) |
|
单调性 |
单调递增 |
单调递减 |
(3)对数函数图象和性质
|
a |
a>1 |
0<a<1 |
|
性质 |
||
|
①定义域:(0,+∞) |
||
|
②值域:R |
||
|
③过点(1,0),即当x=1时,y=0 |
||
|
④在(0,+∞)上是增函数 |
在(0,+∞)上是减函数 |
|
|
⑤x>1时,y>0;0<x<1时,y<0 |
x>1时,y<0;0<x<1时,y>0 |
(4)函数有零点的判定
如果函数y=f(x)在一个区间[a,b]上的图象不间断,并且在它的两个端点处的函数值异号,即f(a)·f(b)<0,则这个函数在这个区间上,至少有一个零点,即存在一点x0∈(a,b),使f(x0)=0,这样的零点叫做变号零点,有时曲线通过零点时不变号,这样的零点叫做不变号零点。
函数的零点、方程的根、函数图象与x轴的交点的横坐标,实质是同一个问题的三种不同表现形式,如方程根的个数就是函数零点的个数,也就是函数图象与x轴的交点个数。
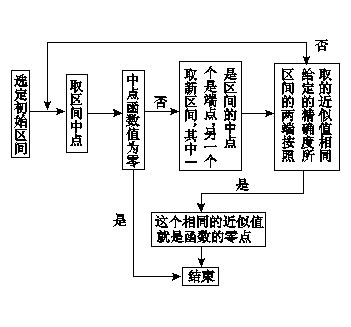
用计算机操作求零点近似值,其操作步骤如图所示:
(5)常见的几种函数模型
①一次函数型y=kx+b;
②反比例函数型y=k/x(k≠0);
③二次函数型y=ax2+bx+c(a≠0);
④指数函数型y=N(1+p)x(增长率问题)(x>0);
⑤y=x+a/x型;
⑥分段函数型。
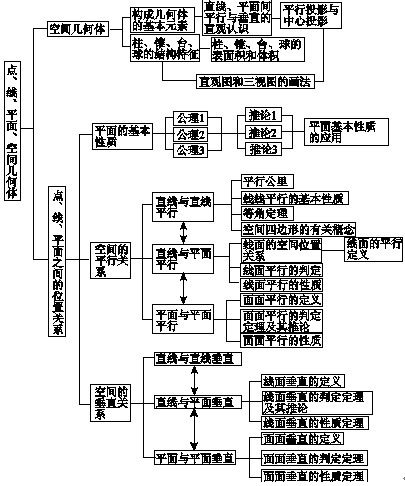
3.立体几何初步
(1)
(2)
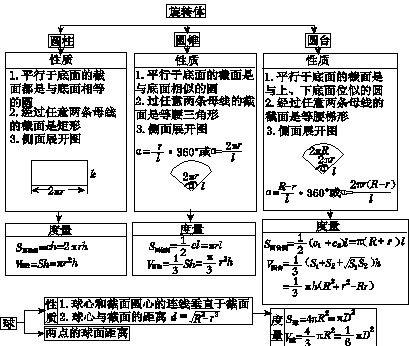
|
性质 |
|
1.平行于底面的截面是与上、下底面全等的正多边形 |
|
度 量 |
|
S棱柱侧=cl |
|
性质 |
|
1.平行于底面的截面是与底面相似的正多边形 |
|
度量 |
|
S棱台侧=(c1+c2)h′ |
(c1、c2为上下底周长,h′为斜高,S1S2为上下底面积,h为高) 棱锥 正棱锥
|
性质 |
|
1.平行底面的截面是与底面相似的正多边形 |
|
度量 |
|
S棱锥侧=1/2ch′ |
(以上体积公式对一般棱锥台均适用)
注:球面距离(球面上经过两点的大圆在这两点间的一段劣弧的长度),计算A、B两点间的球面距离关键是搞清纬度、经度、经度差、纬度差等概念,求球面上两点A、B间的距离的步骤:①计算线段AB的长;②计算球心角AOB的弧度数;③用弧长公式计算劣弧AB的长。
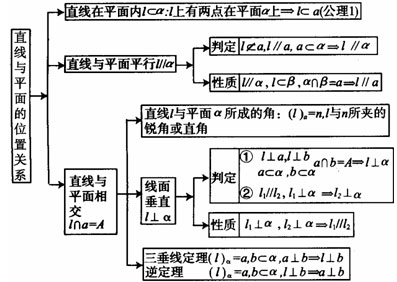
(3)
(上面符号“(l)α=a”表示“直线l在平面α上的射影为a”)
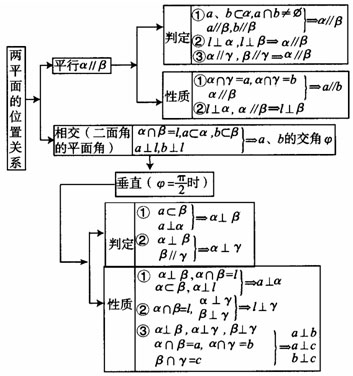
(4)
(5)三视图:选取三个两两垂直的平面作为投射面,一个水平放置,叫做水平投射面,投射到这个平面内的图形叫做俯视图;一个投射面放置在正前方,这个投射面叫做直立投射面,投射到这个平面内的图形叫做主视图;和直立、水平两个投射面都垂直的投射面叫做侧立投射面,通常把这个平面放在直立投影面的右面,投射到这个平面内的图形叫做左视图。将空间图形向这三个平面作正投影,然后把这三个投影按一定的布局放在一个平面内,这样构成的图形叫做空间图形的三视图。
更多高考信息请访问:新浪高考频道 高考论坛 高考博客圈 高考贴吧
特别说明:由于各方面情况的不断调整与变化,新浪网所提供的所有考试信息仅供参考,敬请考生以权威部门公布的正式信息为准。