不支持Flash
|
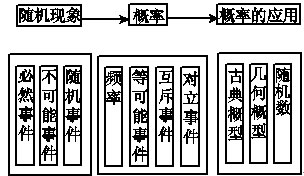
知识大盘点:概率
7.概率
(1)互斥事件与对立事件的概念
若事件A与B不可能同时发生,则称事件A与B互斥。从集合的角度看,事件A,B互斥,表示其相应的集合的交集是空集。
对于事件A,所有不包含在A中的结果组成的集合记为事件,事件A与事件必有一个发生的互斥事件叫做对立事件。从集合的角度看,由事件所含的结果组成的集合组成的集合,是全集I中由事件A所含的结果组成的集合的补集。于是有:A∪=I,A∩=∅.
一般来说,两个对立事件一定是互斥事件,而两个互斥事件却不一定是对立事件。对立事件是互斥事件的特殊情况,两个事件互斥是两个事件对立的必要不充分条件。
(2)古典概型
Ⅰ.古典概型的定义
在试验中,能够描绘其他事件且不能再分的最简单事件是基本事件。
具有特征
①有限性 每次试验可能出现的结果(即基本事件)只有有限个;
②等可能性 每次试验中,各基本事件的发生都是等可能的。
故随机试验的概率模型称为古典概型。
Ⅱ.古典概型的概率公式
如果一次试验中可能出现的结果有n个,而且所有结果出现的可能性都相等,那么每一个基本事件的概率都是。如果某个事件A包含的结果有m个,那么事件A的概率为
P(A)=m/n=A中所含的基本事件数/基本事件总数
根据公式P(A)=m/n进行概率计算时,关键是求出n,m的值,在求n值时,应注意这n种结果必须是等可能的。对一些比较简单的概率问题,求m、n的值只需枚举即可。
Ⅲ.古典概型的集合理解
设在一次试验中,等可能出现的n个结果构成一个集合I,包含m个结果的事件A对应于I的含有m个元素的子集A,则事件A发生的概率为:
P(A)=m/n=card(A)/card(I).
求古典概型的概率要明确两点:①选取适当的集合I,使它满足等可能的要求,找出n值;②把事件A表示为I的某个子集A,找出m值。
(3)几何概型试验
Ⅰ.几何概型试验的定义
如果一个随机试验满足:
①试验结果是无限不可数;
②每个结果出现的可能性是均匀的。
则该试验为几何概型试验。
Ⅱ.几何概型的概率
事件A理解为区域Ω的某一个子区域A,A的概率只与子区域A的几何度量(长度、面积或体积)成正比,而与A的位置和形状无关,满足以上条件的试验称为几何概型,记P(A)=μA/μΩ.
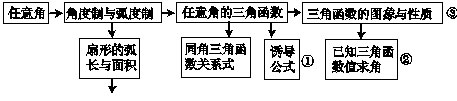
8.基本初等函数(Ⅱ)及三角恒等变换
同角三角函数关系式:
(1)平方关系:sin2α+cos2α=1,1+tan2α=sec2α,1+cot2α=csc2α;
(2)倒数关系:sinαcscα=1,cosαsecα=1,tanαcotα=1;
(3)商数关系:tanα=sinα/cosα,cotα=cosα/sinα.
①诱导公式的规律可简记为:奇变偶不变,符号看象限。此外在应用时,不论α取什么值,我们始终视α为锐角。否则,将导致错误。诱导公式的应用是求任意角的三角函数值,其一般步骤:a.负角变正角,再写成2kπ+α,0≤α<2π;b.转化为锐角。
②求角的方法:先确定角的范围,再求出关于此角的某一个三角函数(要注意选择,其标准有二:一是此三角函数在角的范围内具有单调性;二是根据条件易求出此三角函数值).
③三角函数的图象与性质:
|
三角函数 |
y=sinx |
y=cosx |
y=tanx |
y=cotx |
|
定义域 |
(-∞,+∞) |
(-∞,+∞) |
(nπ-,nπ+) |
(nπ,nπ+π) |
|
值域 |
[-1,1] |
[-1,1] |
(-∞,+∞) |
(-∞,+∞) |
|
最大(小) |
当x=2kπ+ |
当x=2kπ时, |
无 |
无 |
|
奇偶性 |
奇函数 |
偶函数 |
奇函数 |
奇函数 |
|
周期性 |
T=2π |
T=2π |
T=π |
T=π |
|
有界性 |
有界 |
有界 |
无界 |
无界 |
|
单调性 |
在[2kπ-, |
在[(2k-1)π,2kπ] |
在(kπ-, |
在(kπ,kπ+π) |
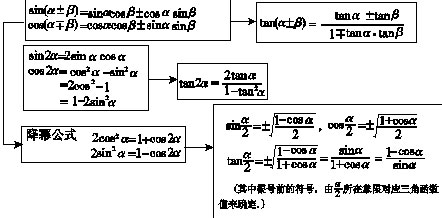
(ⅰ)公式间的关系
相除相除相除
(ⅱ)辅助角公式:asinα+bcosα=√a*a+b*bsin(α+φ)(辅助角φ所在象限由点(a,b)的象限决定,tanφ=b/a).
(ⅲ)三角函数的化简、计算、证明的恒等变形的基本思路是:一角二名三结构。即首先观察角与角之间的关系,注意角的一些常用变式,角的变换是三角函数变换的核心;第二看函数名称之间的关系,通常“切化弦”;第三观察代数式的结构特点。基本的技巧有:
a.巧变角(已知角与特殊角的变换、已知角与目标角的变换、角与其倍角的变换、两角与其和差角的变换。如α=(α+β)-β=(α-β)+β,2α=(α+β)+(α-β),2α=(β+α)-(β-α),α+β=2·α+β/2,α+β/2=α-β/2-α/2-β等).
b.三角函数名互化(切割化弦).
c.公式变形使用如:tanα±tanβ=tan(α+β)(1∓tanαtanβ).
d.三角函数次数的降升(降幂公式:cos2α=1+cos2α/2,sin2α=1-cos2α/2;升幂公式:1+cos2α=2cos2α,1-cos2α=2sin2α).
e.式子结构的转化(对角、函数名、式子结构化同).
f.常值变换主要指“1”的变换(1=sin2x+cos2x=sec2x-tan2x=tanxcotx=tanπ/4=sinπ/2=…).
更多高考信息请访问:新浪高考频道 高考论坛 高考博客圈 高考贴吧
特别说明:由于各方面情况的不断调整与变化,新浪网所提供的所有考试信息仅供参考,敬请考生以权威部门公布的正式信息为准。