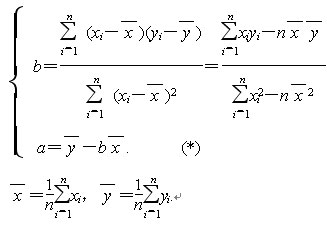4.平面解析几何初步

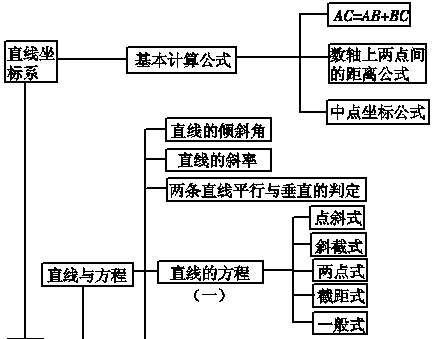
　　(1)直线方程的五种形式

　　①点斜式：已知直线过点(x0，y0)，斜率为k，则直线方程为y－y0＝k(x－x0)，它不包括垂直于x轴的直线；②斜截式：已知直线在y轴上的截距为b，斜率为k，则直线方程为y＝kx＋b，它不包括垂直于x轴的直线；③两点式：已知直线经过P1(x1，y1)，P2(x2，y2)两点，则直线方程为x-x1/x2-x1＝y-y1/y2-y1，它不包括垂直于坐标轴的直线；④截距式：已知直线在x轴和y轴上的截距为a，b，则直线方程为x/a＋y/b＝1，它不包括垂直于坐标轴的直线和过原点的直线；⑤一般式：任何直线均可写成Ax＋By＋C＝0(A，B不同时为0)的形式。

　　注：求直线方程的基本思想和方法是恰当选择方程的形式，利用待定系数法求解。

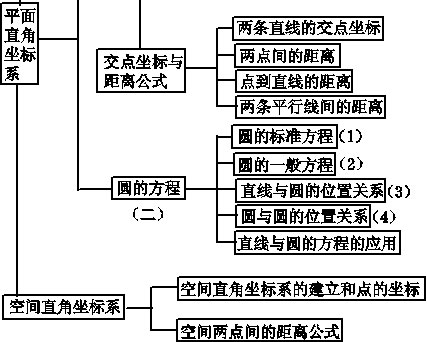
　　(2)①圆的标准方程

　　圆心为(a，b)，半径为r的圆的标准方程为(x－a)2＋(y－b)2＝r2.说明：方程中有三个参量a、b、r，因此三个独立条件可以确定一个圆。

　　②圆的一般方程

　　二次方程x2＋y2＋Dx＋Ey＋F＝0(*)，将(*)式配方得(x＋D/2)2＋(y＋E/2)2＝D*D+E*E-4F/4.

　　当D2＋E2－4F＞0时，方程(*)表示圆心(－D/2，－E/2)，半径r＝1/2√D*D+E*E-4F的圆，把方程x2＋y2＋Dx＋Ey＋F＝0(D2＋E2－4F＞0)叫做圆的一般方程。

　　说明：Ⅰ.圆的一般方程体现了圆方程的代数特点：a.x2、y2项系数相等且不为零.b.没有xy项。

　　Ⅱ.当D2＋E2－4F＝0时，方程(*)表示点(－D/2，－E/2)，当D2＋E2－4F＜0时，方程(*)不表示任何图形。

　　Ⅲ.据条件列出关于D、E、F的三元一次方程组，可确定圆的一般方程。

　　③研究直线与圆的位置关系有两种方法：一是将直线与圆的交点问题转化为研究它们的方程所组成的方程组有几个实数解的问题。通常利用判别式法。若Δ>0有2解，则直线与圆相交；若Δ＝0有1解，则直线与圆相切；若Δ<0，无解，则直线与圆相离。二是将直线与圆的位置关系转化为判定圆心到直线的距离d与半径r大小的比较。若d>r，直线与圆相离；若d＝r，直线与圆相切；若d<r，则直线与圆相交。解析几何通常使用第2种方法。

　　④判定两圆的位置关系的方法有二：第一种是代数法，研究两圆的方程所组成的方程组的解的个数；第二种是研究两圆的圆心距与两圆半径之间的关系。第一种方法因涉及两个二元二次方程组成的方程组，其解法一般较烦琐，故使用较少，通常使用第二种方法，具体如下：

　　圆(x－a1)2＋(y－b1)2＝r与圆(x－a2)2＋(y－b2)2＝r的位置关系，其中r1>0，r2>0.

　　设两圆的圆心距为d，则

　　d＝√(a1-a2)(a1-a2)+(b1-b2)(b1-b2)，

　　当d>r1＋r2时，两圆外离；

　　当d＝r1＋r2时，两圆外切；

　　当|r1－r2|<d<|r1＋r2|时，两圆相交；

　　当d＝|r1－r2|时，两圆内切；

　　当0<d<|r1－r2|时，两圆内含。

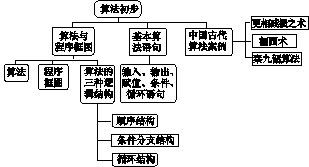
　　5.算法

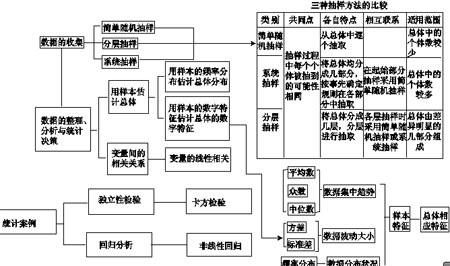
　　6.统计与统计案例

　　求回归直线方程的思想方法

　　在观察散点图特征时，发现各点大致分布在一条直线的附近，画出的直线不止一条类似的直线，应选择最能代表变量x与y之间关系的直线的特征，即n个偏差的平方和最小。设所求直线方程为y＝bx＋a，其中a、b是待定系数，则

　　yi＝bxi＋a　(i＝1,2，…，n)

　　于是得到各个偏差

　　yi－yi＝yi－(bxi＋a)　(i＝1,2，…，n)

　　显见，偏差yi－i的符号有正有负，若将它们相加会造成相互抵消，故采用n个偏差的平方和

　　Q＝ ni＝1(yi－bxi－a)2

　　采用最小二乘法可求出使Q为最小值时的b和a.

　　更多高考信息请访问：新浪高考频道 高考论坛 高考博客圈 高考贴吧

　　特别说明：由于各方面情况的不断调整与变化，新浪网所提供的所有考试信息仅供参考，敬请考生以权威部门公布的正式信息为准。