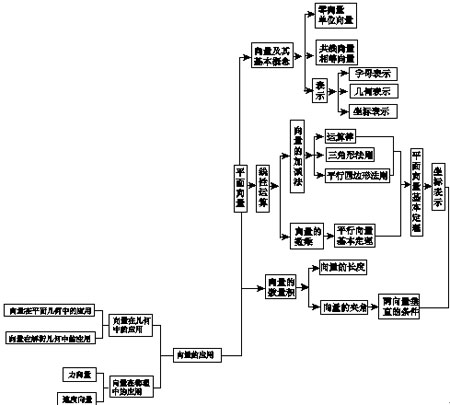
9.平面向量

　　(1)平面向量基本定理，如果e1、e2是同一平面内非共线向量，那么该平面内的任一向量a，有且只有一对实数λ1、λ2使a＝λ1e1＋λ2e2.

　　①两个向量平行的充要条件

　　a∥b⇔a＝λb

　　设a＝(x1，y1)，b＝(x2，y2)

　　a∥b＝x1x2－y1y2＝0

　　②两个非零向量垂直的充要条件

　　a⊥b⇔a·b＝0

　　设a＝(x1，y1)，b＝(x2，y2)

　　a⊥b＝x1x2＋y1y2＝0

　　θ＝〈a，b〉.

　　cosθ＝x1x2＋y1y2/x21＋y21

　　x22＋y22

　　(2)数量积的性质：设e是单位向量，〈a，e〉＝θ

　　①a·e＝e·a＝|a|cosθ；②当a，b同向时，a·b＝|a||b|，特别地，a2＝a·a＝|a|2，|a|＝；当a与b反向时，a·b＝－|a||b|；③a⊥b⇔a·b＝0；④非零向量a，b夹角θ的计算公式：cosθ＝，当θ为锐角时，a·b＞0，且ab不同向，a·b>0是θ为锐角的必要非充分条件；当θ为钝角时，a·b<0，且ab不反向，a·b<0是θ为钝角的必要非充分条件；⑤|a·b|≤|a||b|.

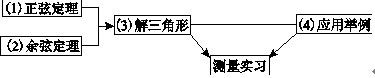
　　10.解三角形

　　(1)正弦定理

　　a/sinA＝b/sinB＝c/sinC＝＝＝2R.

　　正弦定理的三种变式：

　　①a＝2RsinA，b＝2RsinB，c＝2RsinC.

　　②sinA＝a/2r，sinB＝b/2r，sinC＝c/2r.

　　③a∶b∶c＝sinA∶sinB∶sinC.

　　(2)余弦定理

　　a2＝b2＋c2－2bccosA　b2＝a2＋c2－2cacosB

　　c2＝a2＋b2－2abcosC或cosA＝b2＋c2－a2/2bc

　　cosB＝a2＋c2－b2/2ac　cosC＝a2＋b2－c2/2ab

　　余弦定理的特殊情况：

　　①在△ABC中，若a2＜b2＋c2，则0°＜A＜90°；

　　反之，若0°<A<90°，则a2<b2＋c2.

　　②在△ABC中，若a2＝b2＋c2，则A＝90°；

　　反之，若A＝90°，则a2＝b2＋c2.

　　③在△ABC中，若a2>b2＋c2，则90°<A<180°；

　　反之，若90°<A<180°，则a2>b2＋c2.

　　(3)解斜三角形有下表所示的四种情况：

　　在△ABC中，已知a、b和A时，解的情况如下：

　　(4)解斜三角形有着广泛的应用，如测量、航海、几何、物理诸方面都要用到解斜三角形的知识。解此类题的一般步骤是：

　　①阅读理解，画出示意图，分清已知和所求，尤其要理解应用题中有关名词和术语，如坡度、仰角、象限角、方位角等。

　　②分析与所研究的问题有关的一个或几个三角形。

　　③解这些三角形，求出答案。

　　更多高考信息请访问：新浪高考频道 高考论坛 高考博客圈 高考贴吧

　　特别说明：由于各方面情况的不断调整与变化，新浪网所提供的所有考试信息仅供参考，敬请考生以权威部门公布的正式信息为准。