2015国考行测数学运算:植树问题练习题
1. 李大爷在马路边散步,路边均匀地栽着一行树,李大爷从第1棵树走到第15棵树共用了7分钟,李大爷又向前走了几棵树后就往回走,当他回到第5棵树时共用了30分钟。李大爷步行到第几棵树时就开始往回走?
A。第32棵 B. 第33棵 C. 第37棵 D. 第38棵
2. 环保部门对一定时间内的河流水质进行采样,原计划每41分钟采样1次,但在实际采样过程中,第一次和最后一次采样的时间与原计划相同,每两次采样的间隔变成20分钟,采样次数比原计划增加了1倍。问实际采样次数是多少次?
A.22 B.32 C.42 D.52
3.大雪后的一天,小明和爸爸共同步测一个圆形花圃的周长。他俩的起点和走的方向完全相同。小明的平均步长54厘米,爸爸平均步长72厘米。由于两人的脚印有重合,并且他们走了一圈后都回到起点,这时雪地上只留下60个脚印。这个花圃的周长是多少米?
A.15.9 B.16.8 C.17.28 D.21.6
4.有3根相同的木料,打算把每根锯成3段,每锯开一处需要3分钟,全部锯开需多少时间?
A.20 B.15 C.18 D.23
5.运动会上,接受检阅的一列彩车车队共52辆,每辆车长4米,前后每辆车相隔6米,车队每分行驶105米。这列车队要通过536米长的检阅场地,需要多少分钟?
A.4.9 B.8 C.10 D.10.1
![]()
6.一果农想将一块平整的正方形土地分割为四块小的正方形土地,并将果树均匀整齐地种植在土地所有边界上,且在每块土地的四个角上都种上一棵果树。该果农未经细算就购买了60棵果树,如果仍按上述想法种植,那么他至少多买了多少棵果树?
A.0 B.3 C.6 D.15
7.一个四边形广场,它的四边长分别是60米、72米、84米和96米,现在要在四边上植树,四角需种树,而且每两棵树的间隔相等,那么至少要种多少棵树?
A.22 B.25 C.26 D.30
8.用10张同样长的纸条粘接成一条长61厘米的纸条,如果每个接头处都重叠1厘米,那么每张纸条长( )厘米?
A.7 B.6.9 C.6.1 D.7.1
1.【答案】B。中公解析:1-15棵有14个间距,每个间距用时7÷14=0.5分钟。从第15棵回到第5棵走了10个间距,用时5分钟。则他从15棵向前走了(30-5-7)÷0.5÷2=18个间距,步行至第18+15=33棵树往回走。
2.【答案】C。中公解析:设原计划采样x次,有x-1个时间间隔,总用时为41(x-1)分钟。实际采样过程中,第一次和最后一次采样时间与原计划相同说明总用时不变。采样次数变为2x,有2x-1个时间间隔,总用时为20(2x-1)分钟。所以41(x-1)=20(2x-1),x=21次,实际采样次数为42次。
3.【答案】D。中公解析:走完一圈后回到起点,说明花圃周长是54、72的倍数。
54和72 的最小公倍数是216,说明每走216cm父子重合一次,在走216cm的路程中,父亲留下216÷72=3个脚印,小明留下216÷54=4个脚印,因此一共留下3+4-1=6个脚印。
60个脚印要走60÷6=10个216cm。故花园总共长为216×10=2160cm=21.6米。
4.【答案】C。中公解析:锯木头相当于“两端都不植树”问题。
锯成3段需要锯3-1=2次,所以共需3x2x3=18分钟
5. 【答案】C。中公解析:首先应求出车队的长度:车辆总长4×52=208米,前后每辆车车厢隔6米,52辆车中一共有52-1=51个空,总长51×6=306米,因此车队总长为208+306=514米,要完全通过,需要走的路程为车队长度+场地长度=514+536=1050米,因此,一共需要1050÷105=10分钟。
6.【答案】B。中公解析:如下图所示将一块正方形分割为四块小正方形只有这一种分法。在这个问题中,除封闭的大正方形外,中间还有两条线段,按照分式直接套用,会有重复,计算比较复杂,因此转变思路。按照每个角、每条短边分别考虑。
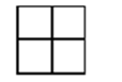
每块土地共种上树的话共有9棵。
共有短边12条,由于果树均匀整齐种植,所以设每边种x棵,则共种树12x+9棵。当x=4时,12x+9=57,与60差距最小,为3棵,因此他至少多买了3棵。
7. 【答案】C。中公解析:如图,这是一个四边形,可从封闭植树考虑。

欲使四个角都要种树,则间距应为60、72、84、96的公约数,要使得种树最少,则应为最大公约数。可求得60、72、84、96的最大公约数为12。即间距为12米。
总路长为四边形的周长=60+72+84+96=312米,棵数=总路长÷间距,则棵数=312÷12=26。
8.【答案】A。中公解析: 10张纸条粘在一起后,有10-1=9个接头,每个接头重叠1厘米,重叠了9厘米,如果不重叠,则共有61+9=70厘米,那么每张长70÷10=7厘米。
本文由中公教育[微博]供稿
- 2015国考行测数学运算:植树问题2014-08-27 11:13
- 公务员行测必考必会:数学运算2014-08-21 15:31
- 2015国考行测数学运算:鸡兔同笼练习题2014-08-20 10:28
- 2015国考行测数学运算:鸡兔同笼问题讲解2014-08-20 10:25
- 国考行测数学运算:容斥和抽屉原理练习2014-08-13 11:22
- 2015国考行测数学运算:容斥和抽屉原理2014-08-13 11:16













閺傜増姘拃锔俱仛閿涙矮鎹㈡担鏇熸暪鐠愬綊顣╁ù瀣兊缁併劋绱伴崨妯肩搼楠炲灝鎲¢惃鍡曡礋鐠囧牓鐛ラ敍宀冾嚞閸曞じ绗傝ぐ鎿勭磼閻愮懓鍤潻娑樺弳鐠囷附鍎�