2015上海公务员考试行测排列组合分析
排列组合问题是每年公务员[微博]考试行测中的必考题型。此类题目是行测数学中唯一一类涉及高中数学的题型,考生初次接触会觉得难度较大,不知如何入手。因此考生备考时要对此类题充分重视,此类题目考查的是思维,擅长的考生能快速解出取得相应分数。中公教育[微博]专家主要针对核心概念和方法技巧这两个方面进行深入讲解。
一、基本概念
1、加法原理:做一件事,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,在第n类办法中有mn种不同的方法,那么完成这件事共有N= m1+ m2+ m3+…+mn种不同方法,每一种方法都能够直接达成目标。
2、乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有N= m1× m2× m3×…×mn种不同的方法。完成一件事必须做好从前至后的每一个步骤。
3、排列和排列数:从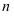 个不同元素中,任取
个不同元素中,任取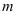 (
(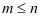 )个元素(这里的被取元素各不相同)按照一定的顺序排成一列,用符号
)个元素(这里的被取元素各不相同)按照一定的顺序排成一列,用符号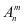 表示。
表示。
4、组合和组合数:一般地,从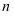 个不同元素中取出
个不同元素中取出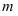
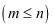 个元素并成一组,无高低顺序之分,用符号
个元素并成一组,无高低顺序之分,用符号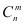 表示。
表示。
5、公式: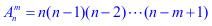 (
(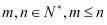 ),阶乘:
),阶乘: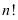 表示正整数1到
表示正整数1到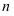 的连乘积,叫做
的连乘积,叫做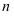 的阶乘
的阶乘 规定
规定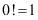 。
。
公式: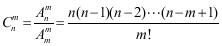 或
或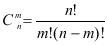
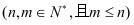
6、组合数的性质1: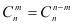 。规定:
。规定: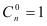 ;性质2:
;性质2: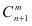 =
=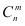 +
+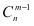
【例1】甲乙两个科室各有4名职员,且男女各半。现从两个科室中选出4人参加培训,要求女职员比重不得低于一半,且每个科室至少选一人,问有多少种不同的选法?
A.67 B.63 C.53 D.51
【答案】D
【中公解析】本题属于计数问题,3分类讨论,因为女职员比重不得低于一半,所以女职工人数有三种情况2人,3人,4人,当女职工有4人时,只有从甲乙两个科室各取2个女职员一种情况,当女职工人数为3人时,从4个女职工中选出3人,再从4个男职工中选出1人,总共是16种情况。当女职工人数为两人时,从4个女职工中选出2人,再从4个男职工中选出2人,总共是36中情况,减去2男2女都来自一个部门的情况共两种,所以是34中,这样把所有情况相加等于1+16+34=51,选D。
【例2】要求厨师从12种主料中挑选出2种、从13种配料中挑选出3种来烹饪某道菜肴,烹饪的方式共有7种,那么该厨师最多可以做出多少道不一样的佳肴?
A.131204 B.132132 C.130468 D.133456
【答案】B
【中公解析】根据题意可知,做菜需要三步,第一步从12种主料中挑选出2种,无顺序之分,有C122种方法;第二步从13种配料中挑选出3种,有C133种方法,第三步从7种烹饪方式中挑选出一种,有7种方法。根据乘法原理,故做菜的方式共有(12×11×13×2×11×7)/2×2×3种,尾数应为2。因此,选B。
【例3】小王忘记了朋友的手机号码的最后两位数字,只记得倒数第一位奇数,则他最多要拨多少次才能保证拨对朋友的手机号码?
A、90 B、50 C、45 D、20
【答案】B
【中公解析】完成此次拨打,要完成最后两位输入,则对应是乘法原理。手机号码的倒数第一位是奇数,则可能的数为1、3、5、7、9,共5个;倒数第二位可以是0、1、2、…9中的任何一个数字,共10个。由此可知,手机号码最后两位的组合形式共有5×10=50种,也就是说,小王最多要拨打50次才能保证打通朋友的电话。因此,选B。
中公教育专家认为,排列组合题目主要考察对基本原理的理解,要做一件事,完成它若是有n类办法,是分类问题,第一类的方法是独立的,要使用加法原理;做一件事,需要分n个步骤,步骤之间是连续的,只有分成若干个互相联系的步骤,依次相继完成这件事才算完成,因此用乘法原理。口诀加法原理:类类独立;乘法原理:步步相关。排列与组合的区别与联系:与顺序无关的为组合问题,与顺序有关的为排列问题,其实排列可以看成两步,首先从n个元素中选出来m个,然后把选出来的m个元素按顺序排列起来,也就是不仅要从n个元素中选出m个,还要知道m个元素是什么。
特别说明:由于各方面情况的不断调整与变化,新浪网所提供的所有考试信息仅供参考,敬请考生以权威部门公布的正式信息为准。
- 2015上海市公务员考试:语病歧义巧解答2014-12-08 14:25
- 2015上海市公务员考试言语模块全面解读2014-12-08 14:24
- 2015上海公务员考试申论热点:文化养老2014-12-08 14:06
- 2015上海公务员考试行测备考指导2014-11-25 11:45
- 2015上海公务员考试常识解题技巧2014-11-24 18:11
- 2015上海公务员考试行测大纲解读2014-11-21 10:27
- “国考”仍难言“降温”只是门槛高了2014-12-03 10:41
- 2011到2015年国家公务员考试报名热门专业2014-12-02 15:25
- 国考五年:国税系统最俏 法律专业最火2014-12-02 15:23
- 时评:以平常心看待公考冷热2014-12-02 11:35
- 国考“双降一升”,多少疑问待解2014-12-02 11:34
- “国考”参考人数跌了10万2014-12-02 11:30


