1.100人参加7项活动，已知每个人只参加一项活动，而且每项活动参加的人数都不一样。那么，参加人数第四多的活动最多有几人参加？

　　A.22            B.21           C.24                D.23

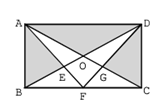
　　2.如图所示，长方形ABCD的两条边长分别为8m和6m，四边形OEFG的面积是4m²，则阴影部分的面积为？                 

　　A.32 m²               B.28 m²    　　C.24 m²              D.20 m²

　　3.某高校对一些学生进行问卷调查。在接受调查的学生中，准备参加注册会计师考试的有63人，准备参加英语六级考试的有89人，准备参加计算机考试的有47人，三种考试都准备参加的有24人，准备选择两种考试参加的有46人，不参加其中任何一种考试的有15人。问接受调查的学生共有多少人？

　　A.120                                   B.144

　　C.177                                   D.192

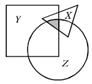
　　4.如图所示，X、Y、Z分别是面积为64、180、160的三张不同形状的纸片。它们部分重叠放在一起盖在桌面上，总共盖住的面积为290。且X与Y、Y与Z、Z与X重叠部分面积分别为24、70、36。问阴影部分的面积是多少？

　　A.15                                  B.16                   

　　C.14                                  D.18

　　5.三位专家为10幅作品投票，每位专家分别都投出了5票，并且每幅作品都有专家投票。如果三位专家都投票的作品列为A等，两位专家投票的列为B等，仅有一位专家投票的作品列为C等，则下列说法正确的是(    )。

　　A.A等和B等共6幅                       B.B等和C等共7幅

　　C.A等最多有5幅                         D.A等比C等少5幅

　　6.将104张桌子分别放到14个办公室，每个人办公室至少放一张桌子，不管怎样分至少有几个办公室的桌子数是一样多？

　　A.2                 B.3               C.7             D。无法确定

　　7.从1，2，3，…，49，50这50个数中取出若干个数，使其中任意两个数的和都不能被7整除，则最多能取出多少个数？

　　A.23           B.24         C.25               D.26

　　8.10个足球队之间共赛了11场，赛得最多的球队至少赛了几场？

　　A.3              B.4             C.6                D.5

　　9.某学校1999名学生去游故宫、景山和北海三地，规定每人至少去一处，至多去两地游览，那么至少有多少人游的地方相同？

　　A.35           B.186          C.247               D.334

　　10.将104张桌子分别放到14个办公室，每个人办公室至少放一张桌子，不管怎样分至少有几个办公室的桌子数是一样多？

　　A.2             B.3             C.7             D。无法确定

　　参考答案：

　　1.【答案】A。中公解析：按不同活动把100人分为7个互斥集合。按参加人数从少到多设为x1，x2，x3，x4，x5，x6，x7。

　　欲令参加人数第四多的活动(x4)人数最多，根据“此消彼长”的原则，参加人数最少的三个活动(x1，x2，x3)的人数应该最少，为1、2、3。参加人数最多的三个活动(x5，x6，x7)人数应尽量少，即x4，x5，x6，x7为公差为1的等差数列。

　　x4+x5+x6+x7=100-1-2-3=94。平均数为94÷4=23.5，利用等差数列知识，易求出x4=22。

　　2.【答案】B。中公解析：矩形ABCD的面积为8×6=48m2，阴影部分面积等于ABCD面积-空白部分面积。三角形BDF面积对应为X，三角形AFC面积对应为Y，则空白部分面积对应为X∪Y，四边形OEFG面积对应为X∩Y。

　　选择容斥原理1，X∪Y=X+Y-X∩Y；所求为48-X∪Y。

　　6.【答案】A。中公解析：求至少有几个办公室桌子数一样，即求有几个抽屉中物品一样多。可从任意的办公室桌子不同构造抽屉。

　　若要让办公室中桌子数不同，可以每个办公室分别为1、2、3、4、…、13、14张，那么14个房间需要(1+14)×14÷2=105张，因此只能有一个办公室中桌子数减少105-104=1张，故最少有2个办公室的桌子数是一样的。

　　7.【答案】A。中公解析：考查利用数的性质构造抽屉。

　　将1，2，3，…，49，50这50个数，按除以7的余数分为7个抽屉：余数为0，1，2，3，4，5，6，其所含的数的个数分别为7，8，7，7，7，7，7。

　　被7除余1与余6的两个数之和是7的倍数，所以取出的数只能是这两种之一；

　　同理，被7除余2与余5的两个数之和是7的倍数，所以取出的数只能是这两种之一；被7除余3与余4的两个数之和是7的倍数，所以取出的数只能是这两种之一；

　　两个数都是7的倍数，它们的和也是7的倍数，所以7的倍数中只能取1个。

　　因此最多可以取出8+7+7+1=23个

　　8.【答案】A。中公解析：求同一抽屉中最多的物品数，利用抽屉原理解题。

　　因为每场球赛有2个球队参加，所以11场球赛共有11×2=22队次参加，把10个足球队看成10个抽屉，由于22÷10=2……2(n=10，m=2)，根据抽屉原理2，赛得最多的球队至少赛了2+1=3场比赛。

　　10.【答案】A。中公解析：求至少有几个办公室桌子数一样，即求有几个抽屉中物品一样多。可从任意的办公室桌子不同构造抽屉。

　　若要让办公室中桌子数不同，可以每个办公室分别为1、2、3、4、…、13、14张，那么14个房间需要(1+14)×14÷2=105张，因此只能有一个办公室中桌子数减少105-104=1张，故最少有2个办公室的桌子数是一样的。