61. 某农场有36台收割机，要收割完毕所有的麦子需要14天时间，现在收割了7天后增加4台收割机，并通过技术改造使每台收割机的效率提升5%。问收割完成所有的麦子还需要几天？(    )

　　A. 3            B. 4            C. 5            D. 6

　　【京佳解析】 D    工程问题。假设收割完成所有的麦子还需要t天，1台收割机1天的工作效率为1，则有：36×14×1－36×7×1＝(36＋4)×1×(1＋5%)×t，解得t＝6天。故选D。

　　62. 某单位有50人，男女性别比为3：2，其中15人未入党，如从中任选1人，则此人为男性党员的概率最大为多少？(    )

　　A. 35            B. 23            C. 34            D. 57

　　【京佳解析】 A    极值问题(与概率问题相关)。由“男女性别比为3：2”得，男性有30人；由“15人未入党”得，党员有35人，则男性党员最多有30人；因此，任选1人为男性党员的概率最大为30÷50＝3/5。故选A。

　　63. 某技校安排本届所有毕业生分别去甲、乙、丙3个不同的工厂实习。去甲厂实习的毕业生占毕业生总数的32%，去乙厂实习的毕业生比甲厂少6人，且占毕业生总数的24%。问去丙厂实习的人数比去甲厂实习的人数(    )。

　　A. 少9人         B. 多9人         C. 少6人         D. 多6人

　　【京佳解析】 B    比例问题。根据“去甲厂实习的毕业生占毕业生总数的32%，去乙厂实习的毕业生比甲厂少6人，且占毕业生总数的24%”可得，总人数为6÷(32%－24%)＝75人；则去甲厂实习的有75×32%＝24人，去丙厂实习的有75×(1－32%－24%)＝33人；因此，去丙厂实习的人数比去甲厂实习的人数多9人。故选B。

　　64. 甲、乙、丙、丁四人共同投资一个项目，已知甲的投资额比乙、丙二人的投资额之和高20%，丙的投资额是丁的60%，总投资额比项目的资金需求高1/3。后来丁因故临时撤资，剩下三人的投资额之和比项目的资金需求低1/12。则乙的投资额是项目资金需求的(    )。

　　A. 16            B. 15            C. 14            D. 13

　　【京佳解析】 A    比例问题。设项目的资金需求为m，丁的投资额为n，那么四人的总投资额为43m，则有：43m－n＝(1－112)m，解得n＝512m；由“丙的投资额是丁的60%”可得，丙的投资额为512m×60%＝312m；再设甲和乙的投资额分别为x和y，则有：x＝(y＋312m)×(1＋20%)，x＋y＝43m－512m－312m，解得x＝12m，y＝16m；因此，乙的投资额是项目资金需求的16。故选A。

　　66. 把12棵同样的松树和6棵同样的柏树种植在道路两侧，每侧种植9棵，要求每侧的柏树数量相等且不相邻，且道路起点和终点处两侧种植的都必须是松树。问有多少种不同的种植方法？(    )

　　A. 36            B. 50            C. 100            D. 400

　　【京佳解析】 C    排列组合问题。由题意知，安排方法是把松树和柏树分别分成两堆，每堆分别为6棵和3棵；正确的栽种方法是：先把松树分别栽到道路的两边，然后把柏树插空进去，共有方法C³₅×C³₅＝100种。故选C。

　　67. 餐厅需要使用9升食用油，现在库房里库存有15桶5升装的，3桶2升装的，8桶1升装的。问库房有多少种发货方式，能保证正好发出餐厅需要的9升食用油？(    )

　　A. 4            B. 5            C. 6            D. 7

　　【京佳解析】 C    基本运算。采用枚举法求解，由题意得，9升的油可以有如下几种组合：(1)1桶5升、2桶2升；(2)1桶5升、1桶2升、2桶1升；(3)1桶5升、4桶1升；(4)3桶2升、3桶1升；(5)2桶2升、5桶1升；(6)1桶2升、7桶1升；共计6种。故选C。

　　68. 小李的弟弟比小李小2岁，小王的哥哥比小王大2岁、比小李大5岁。1994年，小李的弟弟和小王的年龄之和为15。问2014年小李与小王的年龄分别为多少岁？(    )

　　A. 25，32         B. 27，30         C. 30，27         D. 32，25

　　【京佳解析】 B    年龄问题。由“小王的哥哥比小王大2岁、比小李大5岁”可知，小王比小李大3岁，选项中只有B项符合。故选B。

　　69. 现在要在一块长25公里、宽8公里的长方形区域内设置哨塔，每个哨塔的监视半径为5公里。如果要求整个区域内的每个角落都能被监视到，则至少需要设置多少个哨塔？(    )

　　A. 4            B. 5            C. 6            D. 7

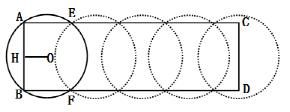
　　【京佳解析】B    极值问题。长方形区域的总面积为25×8＝200平方公里，假设长方形的四个顶点分别为A、B、C、D，如下图所示，要使得“整个区域内的每个角落都能被监视到”，则第一个塔哨的设置必须将A和B包括在内；设第一个塔哨监视范围为以O为圆心的圆，且与长方形相交于A、B、F、E四点，那么，由“OA＝OB＝OF＝OE＝5，AB＝8”可得，O到AB的直线距离OH为3，则矩形ABFE覆盖到的面积为8×6＝48平方公里；依次类推，至少需要200÷48≈5个圆，才能将长方形所有区域覆盖到，即至少需要设置5个塔哨。故选B。

　　72. 巡检员小刘负责甲、乙、丙三个机房的巡检工作，甲、乙和丙机房分别需要每隔2天、4天和7天巡检一次。3月1日，小刘巡检了3个机房，问他整个3月有几天不用做机房的巡检工作？(    )

　　A. 12               B. 13               C. 14               D. 15

　　【京佳解析】C    周期问题。用枚举法求解，“每隔2天”即每3天，整个3月小刘巡检甲机房的日期为：1、4、7、10、13、16、19、22、25、28、31共计11天；巡检乙机房的日期为：1、6、11、16、21、26、31共计7天；巡检丙机房的日期为：1、9、17、25共计4天；因此，不用做巡检工作的日期为：2、3、5、8、12、14、15、18、20、23、24、27、29、30共计14天。故选C。

　　73. 某企业调查用户从网络获取信息的习惯，问卷回收率为90%。调查对象中有179人使用搜索引擎获取信息，146人从官方网站获取信息，246人从社交网站获取信息，同时使用这三种方式的有115人，使用其中两种的有24人，另有52人这三种方式都不使用。问这次调查共发出了多少份问卷？(    )

　　A. 310            B. 360            C. 390            D. 410

　　【京佳解析】 D    集合问题。本题考查三集合知识，由三集合公式可知，回收试卷总数为179＋146＋246－24－2×115＋52＝369份；因此，这次调查共发出了369÷90%＝410份试卷。故选D。

　　74. 某学校准备重新粉刷升国旗的旗台，该旗台由两个正方体上下叠加而成，边长分别为1米和2米。问需要粉刷的面积为(    )。

　　A. 30平方米         B. 29平方米         C. 26平方米         D. 24平方米

　　【京佳解析】 D    几何问题。旗台的表面积为两个正方体的表面积－小正方体与大正方体叠在一起的面积－大正方体在地面的面积，即：6×1×1＋6×2×2－2×1×1－1×2×2＝24平方米。故选D。